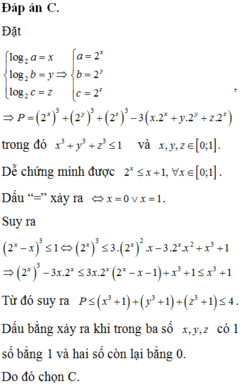Cho a,b,c là các số thực ko âm thỏa mãn a+b+c=3. Tìm GTNN của biểu thức Q=a3 +b3 +c3

Những câu hỏi liên quan
Cho a, b, c là các số thực không âm thỏa mãn \(a^2+b^{2^{ }}+c^{2^{ }}=3\). Tìm giá trị nhỏ nhất và lớn nhất của P = a3 + b3 + c3.
Lời giải:
Tìm min:
Áp dụng BĐT AM-GM:
$a^3+a^3+1\geq 3a^2$
$b^3+b^3+1\geq 3b^2$
$c^3+c^3+1\geq 3c^2$
$\Rightarrow 2(a^3+b^3+c^3)+3\geq 3(a^2+b^2+c^2)$
$\Leftrightarrow 2P+3\geq 9$
$\Leftrightarrow P\geq 3$
Vậy $P_{\min}=3$ khi $(a,b,c)=(1,1,1)$
----------------
Tìm max:
$a^2+b^2+c^2=3\Rightarrow a^2,b^2,c^2\leq 3$
$\Rightarrow a,b,c\leq \sqrt{3}$
Do đó: $a^3-\sqrt{3}a^2=a^2(a-\sqrt{3})\leq 0$
$\Rightarrow a^3\leq \sqrt{3}a^2$
Tương tự với $b,c$ và cộng theo vế:
$P\leq \sqrt{3}(a^2+b^2+c^2)=3\sqrt{3}$
Vậy $P_{\max}=3\sqrt{3}$ khi $(a,b,c)=(\sqrt{3},0,0)$ và hoán vị.
Đúng 2
Bình luận (0)
Cho a, b, c, d là các số thực thỏa mãn 0 ≤ a, b, c ≤ 1. Tìm giá trị lớn nhất của biểu thức T = 2( a3 + b3 + c3 ) – ( a2b + b2c + c2a ).
Do \(0\le a,b,c\le1\)
nên\(\left\{{}\begin{matrix}\left(a^2-1\right)\left(b-1\right)\ge0\\\left(b^2-1\right)\left(c-1\right)\ge0\\\left(c^2-1\right)\left(a-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b-b-a^2+1\ge0\\b^2c-c-b^2+1\ge0\\c^2a-a-c^2+1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b\ge a^2+b-1\\b^2c\ge b^2+c-1\\c^2a\ge c^2+a-1\end{matrix}\right.\)
Ta cũng có:
\(2\left(a^3+b^3+c^3\right)\le a^2+b+b^2+c+c^2+a\)
Do đó \(T=2\left(a^3+b^3+c^3\right)-\left(a^2b+b^2c+c^2a\right)\)
\(\le a^2+b+b^2+c+c^2+a\)\(-\left(a^2+b-1+b^2+c-1+c^2+a-1\right)\)
\(=3\)
Vậy GTLN của T=3, đạt được chẳng hạn khi \(a=1;b=0;c=1\)
Đúng 1
Bình luận (1)
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1
. Khi biểu thức P a3 + b3 + c3 - 3(log2aa + log2bb + log2cc) đạt giá trị lớn nhất thì gi...
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1 . Khi biểu thức P = a3 + b3 + c3 - 3(log2aa + log2bb + log2cc) đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 2
B. 3 . 2 1 3 3
C. 4
D. 6
Đáp án C
Nhận xét, với x ∈ [1;2] thì f(x) = x - log2x ≤ 0. Thật vậy, xét f ' ( x ) = x ln 2 - 1 x ln 2

Từ đây suy ra
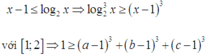
Mặt khác cũng có
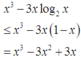
với [1;2]
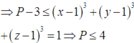
Đúng 0
Bình luận (0)
Cho a,b,c là các số thực thuộc đoạn [1;2] thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1
. Khi biểu thức
P
a
3
+
b
3
+
c
3
-
(...
Đọc tiếp
Cho a,b,c là các số thực thuộc đoạn [1;2] thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1 . Khi biểu thức P = a 3 + b 3 + c 3 - ( log 2 a a + log 2 b b + log 2 c c ) đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
Cho
a
,
b
,
c
là các số thực thuộc đoạn
1
;
2
thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1.
Khi biểu thức
P
a...
Đọc tiếp
Cho a , b , c là các số thực thuộc đoạn 1 ; 2 thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1. Khi biểu thức P = a 3 + b 3 + c 3 − 3 log 2 a a + log 2 b b + log 2 c c đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 2
B. 3.2 1 3 3
C. 4
D. 6
Đáp án C
Nhận xét, với x ∈ 1 ; 2 thì f x = x − log 2 x ≤ 0 . Thật vậy, xét f ' x = x ln 2 − 1 x ln 2
→ f ' x = 0 ⇔ x = 1 ln 2 ⇒ max 1 ; 2 f x = max f 1 , f 1 ln 2 , f 2 = 0
Từ đây suy ra x − 1 ≤ log 2 x ⇒ log 2 3 x ≥ x − 1 3 với 1 ; 2 ⇒ 1 ≥ a − 1 3 + b − 1 3 + c − 1 3
Mặt khác cũng có x 3 − 3 x log 2 x ≤ x 3 − 3 x 1 − x = x 3 − 3 x 2 + 3 x với 1 ; 2
⇒ P − 3 ≤ x − 1 3 + y − 1 3 + z − 1 3 = 1 ⇒ P ≤ 4
Đúng 0
Bình luận (0)
cho a,b,c là 3 số dương thỏa mãn: a+b+c=2019. Tìm GTNN : a3/a2+b2+ab + b3/b2+c2+bc + c3/c2+a2+ca
Đặt \(P=\dfrac{a^3}{a^2+b^2+ab}+\dfrac{b^3}{b^2+c^2+bc}+\dfrac{c^3}{c^2+a^2+ca}\)
Ta có: \(\dfrac{a^3}{a^2+b^2+ab}=a-\dfrac{ab\left(a+b\right)}{a^2+b^2+ab}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^3b^3}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+c^2+bc}\ge\dfrac{2b-c}{3}\) ; \(\dfrac{c^3}{c^2+a^2+ca}\ge\dfrac{2c-a}{3}\)
Cộng vế:
\(P\ge\dfrac{a+b+c}{3}=673\)
Dấu "=" xảy ra khi \(a=b=c=673\)
Đúng 0
Bình luận (0)
xét ba số thực a,b,c thỏa mãn 0 ≤ a,b,c ≤ 2 và a+b+c = 3. Tìm giá trị nhỏ nhất của biểu thức : P = a3+ b3+ c3 + \(\dfrac{\left(ab+bc+ca\right)^3+8}{ab+bc+ca}\)
1,cho các số thực a,b,c ko âm thỏa mãn : a+b+c=3. Tìm GTLN của biểu thức : Q= (a^2-ab+b^2)(b^2-bc+c^2)(c^2-ca+a^2)
2,cho số thực \(a\ge4\).Tìm GTNN của biểu thức S= \(a+\frac{1}{a}\)
2) \(S=a+\frac{1}{a}=\frac{15a}{16}+\left(\frac{a}{16}+\frac{1}{a}\right)\)
Áp dụng BĐT AM-GM ta có:
\(S\ge\frac{15a}{16}+2.\sqrt{\frac{a}{16}.\frac{1}{a}}=\frac{15.4}{16}+2.\sqrt{\frac{1}{16}}=\frac{15}{4}+2.\frac{1}{4}=\frac{15}{4}+\frac{1}{2}=\frac{15}{4}+\frac{2}{4}=\frac{17}{4}\)
\(S=\frac{17}{4}\Leftrightarrow a=4\)
Vậy \(S_{min}=\frac{17}{4}\Leftrightarrow a=4\)
Đúng 0
Bình luận (0)
kudo shinichi sao cách làm giống của thầy Hồng Trí Quang vậy bạn?
\(S=a+\frac{1}{a}=\frac{15}{16}a+\left(\frac{a}{16}+\frac{1}{a}\right)\ge\frac{15}{16}a+2\sqrt{\frac{1.a}{16.a}}=\frac{15}{16}a+2.\frac{1}{4}\)
\(=\frac{15}{16}.4+\frac{1}{2}=\frac{17}{4}\Leftrightarrow a=4\)
Dấu "=" xảy ra khi a = 4
Vậy \(S_{min}=\frac{17}{4}\Leftrightarrow a=4\)
Đúng 0
Bình luận (0)
Cho a,b,c là các số thỏa mãn điều kiện a+b+c=1 và a3+b3+c3=1.
Tính giá trị biểu thức T=a2023+b2023+c2023
\(a+b+c=1\)
\(\Leftrightarrow\left(a+b+c\right)^3=1\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)
\(\Leftrightarrow1+3\left(a+b\right)\left(b+c\right)\left(c+a\right)=1\)'
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0\\b+c=0\\c+a=0\end{matrix}\right.\)
Không mất tính tổng quát, giả sử \(a+b=0\), các trường hợp còn lại làm tương tự.
Khi đó từ \(a+b+c=1\) suy ra \(c=1\) (thỏa mãn). Thế thì \(T=0^{2023}+0^{2023}+1^{2023}=1\).
Như vậy \(T=1\)
Đúng 2
Bình luận (0)
Cho a,b,c là các số thực không âm thỏa mãn a+b+c=3.
Tìm GTNN của biểu thức: \(Q=a^3+b^3+c^3\)
Ta co:
\(Q=a^3+b^3+c^3=\left(a^3+1+1\right)+\left(b^3+1+1\right)+\left(c^3+1+1\right)-6\ge3\left(a+b+c\right)-6=3\)
Dau '=' xay ra khi \(a=b=c=1\)
Vay \(Q_{min}=3\)khi \(a=b=c=1\)