Tìm tham số a để hàm số y=. x + 2a\ √x-a+1 xác định trên (−1;0)

Những câu hỏi liên quan
y= \(\dfrac{mx}{\sqrt{x-m+2}+1}\)
a, Tìm tập xác định của hàm số theo tham số m
b, Tìm m để hàm số có tập xác định trên (0;1)
cho hàm sô y= (m+1)x - 21 (m là tham số,m khác -1 )
a ) xác định m để hàm số trên là hàm sô nghịch biến?
b) xác định m để đồ thị hàm sô trên đi qua điểm A(2;1)?
a: Để hàm số nghịch biến thì m+1<0
hay m<-1
Đúng 0
Bình luận (0)
cho hàm sô y= (m+1)x - 21 (m là tham số,m khác -1 )
a ) xác định m để hàm số trên là hàm sô nghịch biến?
b) xác định m để đồ thị hàm sô trên đi qua điểm A(2;1)?
a: Để hàm số nghịch biến thì m+1<0
hay m<-1
Đúng 0
Bình luận (0)
Vẽ đồ thị (P) hàm số y = 1/4 x2
Tìm các tham số thực m để hai đường thẳng y = 2x và y = (m2 + m ) x + 1 cắt nhau.
Tìm các số thực a để biểu thức 1/√a - 2 + √6 - 2a xác định.
Cho hàm số y=(4-2a)x+b
a, Tìm a để hàm số nghịch biến trên R
b, Xác định của hàm số là đường thẳng song song với đường thẳng y=2x+1 và đi qua điểm C(-1;2)
a)Để hàm số nghịch biến trên R thì 4-2a<0
<=>4<2a
<=>2<a
Vậy a>2 thì hàm số nghịch biến trên R
b)Để hàm số y=(4-2a)x+b là đường thẳng song song với đường thẳng y=2x+1 thì
4-2a=2 và b \(\ne\) 1
<=>a=1 và b \(\ne\) 1 (1)
Để hàm số y=(4-2a)x+b đi qua C(-1;2) thì x=-1 và y=2 (2)
Thay(1),(2)vào hàm số y=(4-2a)x+b
=>2=2(-1)+b
<=>b=4(TMĐK)
Vậy hàm số cần tìm là y=2x+4
a) Để hàm số nghịch biến \(\Leftrightarrow\)4-2a >0\(\Leftrightarrow\)a<2
b) Hai đường thẳng song song với nhau khi và chỉ khi
\(\Leftrightarrow\)4-2a=2 và b khác 1
\(\Leftrightarrow\)a=1 ( b khác 1)
Ta có hàm số y=2x+b
Đồ thị hàm số y=2x+b lại đi qua điểm C (-1;2) nên 2=2.(-1) +b \(\Leftrightarrow\)b=4 (thỏa mãn b khác 1)
Hàm số phải tìm là y=2x+4
Tìm tất cả giá trị của tham số m để hàm số
y
x
-
m
+
2
x
-
m
-
1
xác định trên
0
;
+
∞
. A.
m
≤
1
B.
m
≥
1
C. m 1 D.
m
≤
-
1
Đọc tiếp
Tìm tất cả giá trị của tham số m để hàm số y = x - m + 2 x - m - 1 xác định trên 0 ; + ∞ .
A. m ≤ 1
B. m ≥ 1
C. m < 1
D. m ≤ - 1
Chọn đáp án D
Hàm số xác định khi
![]()

Do đó hàm số đã cho xác định trên 0 ; + ∞
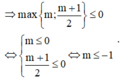
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
−
m
+
1
+
2
x
−
x
+
2
m
xác định trên khoảng (−1;3). A. Không có giá trị m thỏa mãn B.
m
≥
2
C.
m
≥
3
D. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x − m + 1 + 2 x − x + 2 m xác định trên khoảng (−1;3).
A. Không có giá trị m thỏa mãn
B. m ≥ 2
C. m ≥ 3
D. m ≥ 1
cho hàm số bậc nhất \(y=\left(m-1\right)x+3\). Tìm các giá trị của tham số m để hàm số đồng biến trên tập xác định
Để hàm số đồng biến thì m-1>0
=>m>1
Đúng 0
Bình luận (0)
Tìm giá trị của tham số m để hàm số \(y=\dfrac{1}{\sqrt{x^2-2x-m}}\) xác định trên [2; 3]
Hàm xác định trên \(\left[2;3\right]\) khi và chỉ khi:
\(x^2-2x-m>0;\forall x\in\left[2;3\right]\)
\(\Rightarrow x^2-2x>m;\forall x\in\left[2;3\right]\)
\(\Rightarrow m< \min\limits_{\left[2;3\right]}\left(x^2-2x\right)\)
Xét hàm \(f\left(x\right)=x^2-2x\) trên \(\left[2;3\right]\)
\(-\dfrac{b}{2a}=1\notin\left[2;3\right]\)
\(f\left(2\right)=0\) ; \(f\left(3\right)=3\)
\(\Rightarrow\min\limits_{\left[2;3\right]}\left(x^2-2x\right)=0\)
\(\Rightarrow m< 0\)
Đúng 1
Bình luận (6)

















