chứng minh công thức \(a=\frac{-v_0^2}{2s}\)

Những câu hỏi liên quan
từ (1), (2) => (3)
\(v=v_0+at\) (1)
\(t=\frac{v-v_0}{a}\) (2)
=> \(x=2t^2+2t\)
\(x_0=?\)
\(v_0=?\)
a=?
Chứng minh công thức:\(\frac{2}{a\left(a+1\right)\left(a+2\right)}=\frac{1}{a\left(a+1\right)}-\frac{1}{\left(a+1\right)\left(a+2\right)}\)
Ta có: \(\frac{1}{a\left(a+1\right)}-\frac{1}{\left(a+1\right)\left(a+2\right)}=\frac{a+2}{a\left(a+1\right)\left(a+2\right)}-\frac{a}{a\left(a+1\right)\left(a+2\right)}\)
\(=\frac{a+2-a}{a\left(a+1\right)\left(a+2\right)}=\frac{2}{a\left(a+1\right)\left(a+2\right)}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Chứng minh công thức: \(\frac{2}{a\left(a+1\right)\left(a+2\right)}=\frac{1}{a\left(a+1\right)}-\frac{1}{\left(a+1\right)\left(a+2\right)}\)
Có: \(\frac{2}{a\left(a+1\right)\left(a+2\right)}=\frac{\left(a+2\right)-a}{a\left(a+1\right)\left(a+2\right)}=\frac{a+2}{a\left(a+1\right)\left(a+2\right)}-\frac{a}{a\left(a+1\right)\left(a+2\right)}\)\(=\frac{1}{a\left(a+1\right)}-\frac{1}{\left(a+1\right)\left(a+2\right)}\)
Đúng 0
Bình luận (0)
Có: \(\frac{2}{a\left(a+1\right)\left(a+2\right)}=\frac{2+\left(a-a\right)}{a\left(a+1\right)\left(a+2\right)}=\frac{2+a}{a\left(a+1\right)\left(a+2\right)}-\frac{a}{a\left(a+1\right)\left(a+2\right)}\):
Rút gọn các phân số, ta được: \(\frac{1}{a\left(a+1\right)}-\frac{1}{\left(a+1\right)\left(a+2\right)}\)
Bạn hiểu chưa?
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\hat B = {75^0};\hat C = {45^0}\) và \(a = BC = 12\;cm\).
a) Sử dụng công thức \(S = \frac{1}{2}ab.\sin C\) và định lí sin, hãy chứng minh diện tích của tam giác \(ABC\;\)cho bởi công thức \(S = \frac{{{a^2}\sin B\sin C}}{{2\sin A}}\)
b) Sử dụng kết quả ở câu a và công thức biến đổi tích thành tổng, hãy tính diện tích S của tam giác ABC.
a) Theo định lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \to b = \frac{{a.\sin B}}{{\sin A}}\) thay vào \(S = \frac{1}{2}ab.\sin C\) ta có:
\(S = \frac{1}{2}ab.\sin C = \frac{1}{2}a.\frac{{a.\sin B}}{{\sin A}}.sin C = \frac{{{a^2}\sin B\sin C}}{{2\sin A}}\) (đpcm)
b) Ta có: \(\hat A + \hat B + \hat C = {180^0} \Rightarrow \hat A = {180^0} - {75^0} - {45^0} = {60^0}\)
\(S = \frac{{{a^2}\sin B\sin C}}{{2\sin A}} = \frac{{{{12}^2}.\sin {{75}^0}.\sin {{45}^0}}}{{2.\sin {{60}^0}}} = \frac{{144.\frac{1}{2}.\left( {\cos {{30}^0} - \cos {{120}^0}} \right)}}{{2.\frac{{\sqrt 3 }}{2}\;}} = \frac{{72.(\frac{{\sqrt 3 }}{2}-\frac{{-1 }}{2}})}{{\sqrt 3 }} = 36+12\sqrt 3 \)
Đúng 0
Bình luận (0)
Chứng minh công thức :
\(\frac{1}{x}-\frac{1}{x+1}=\frac{a}{x.\left(x+a\right)}\)
1/x-1/x+1=a/x.(x+a)
ta có : 1/x-1/x+1=(x+1)-x/x.(x+1)=1/x.(x+1)
Vay ....
Đúng 0
Bình luận (0)
Chứng minh
Định lý cosin: \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
Công thức tính diện tích: \(S\Delta ABC=\frac{a.h_a}{2}=\frac{a.b.sinC}{2}\)
\(AA'=c.sinB=b.sinC\Leftrightarrow\frac{c}{sinC}=\frac{b}{sinB}.\)
va\(BB'=c.sinA=a.sinC\Leftrightarrow\frac{c}{sinC}=\frac{a}{sinA}\)
\(\Leftrightarrow\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\)
\(S_{\Delta ABC}=\frac{1}{2}.a.AA'=\frac{1}{2}.a.bsinC\)
Đúng 0
Bình luận (0)
Chứng minh
Định lý cosin: \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
Công thức tính diện tích: \(S_{\Delta ABC}\frac{1}{2}a.h_a=\frac{1}{2}ab.sinC\)
Tham khảo:

Chứng minh định lý hàm cos
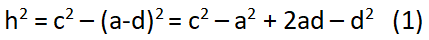
Chứng minh định lý hàm cos – Phương trình 1
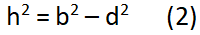
Chứng minh định lý hàm cos – Phương trình 2

Chứng minh định lý hàm cos – Phương trình 3
Với d = b cosC thế vào phương trình biến đổi (3) ta rút ra điều phải chứng minh!
Đúng 0
Bình luận (0)
Chứng minh công thức diện tính tam giác: \(S\Delta ABC=\frac{1}{2}.a.b.SinC=\frac{1}{2}.c.b.SinA=\frac{1}{2}.a.c.SinB\)
Chứng minh công thức \(\overrightarrow F = \frac{{\Delta \overrightarrow p }}{{\Delta t}}\) (19.1).
Xét một vật có khối lượng m không đổi trong suốt quá trình chuyển động. Khi vật chịu tác dụng bởi một lực không đổi \(\overrightarrow F \) thì gia tốc của vật là \(\overrightarrow a \)
Theo định luật II Newton, ta có:
\(\overrightarrow F = m.\overrightarrow a = m.\frac{{\Delta \overrightarrow v }}{{\Delta t}} = \frac{{\Delta \overrightarrow p }}{{\Delta t}}\)
=> đpcm
Đúng 0
Bình luận (0)

















