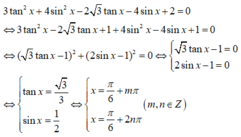√3 tanx - 1 =4sinx
tìm sin x (loại bài giải pt lượng giác)

Những câu hỏi liên quan
giải pt lượng giác:cos2x/cosx+(1+cos^2(x))tanx=1+sin^2(x)
A, sin2 x- 4sinx +3=0
B, 2cos2x- cosx-1=0
C, 3sin2x- 2cosx +2=0
D, 3cosx+ cos2x -cos3x +1=2sinx.sin2x
E, tan2 x+(\(\sqrt{3}\) +1)tanx-\(\sqrt{3}\)=0
F, \(\dfrac{\sqrt{3}}{sin^2x}\)=3cotx + \(\sqrt{3}\)
a, \(sin^2x-4sinx+3=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow sinx=1\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Đúng 1
Bình luận (0)
b, \(2cos^2-cosx-1=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c, \(3sin^2x-2cosx+2=0\)
\(\Leftrightarrow3-3sin^2x+2cosx-5=0\)
\(\Leftrightarrow3cos^2x+2cosx-5=0\)
\(\Leftrightarrow\left(cosx-1\right)\left(3cosx+5\right)=0\)
\(\Leftrightarrow cosx=1\)
\(\Leftrightarrow x=k2\pi\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải PT lượng giác:
`sin(x/2-sinx)=sin^2(x/2)`
Giair các pt lượng giác sau:
1) sinleft(x-frac{pi}{4}right)left(2cos+sqrt{2}right)tan2x0
2) tan2x.sinx+3left(sin-sqrt{3}tan2xright)-3sqrt{3}0
3) frac{cos2x}{sinleft(x+frac{3pi}{4}right)}frac{sinleft(x+frac{3pi}{4}right)}{cos2x}
4) left(frac{tanx-1}{tanx+1}+cot2xright)left(3tan-sqrt{3}right)0;0 x pi
Đọc tiếp
Giair các pt lượng giác sau:
1) \(sin\left(x-\frac{\pi}{4}\right)\left(2cos+\sqrt{2}\right)tan2x=0\)
2) \(tan2x.sinx+3\left(sin-\sqrt{3}tan2x\right)-3\sqrt{3}=0\)
3) \(\frac{cos2x}{sin\left(x+\frac{3\pi}{4}\right)}=\frac{sin\left(x+\frac{3\pi}{4}\right)}{cos2x}\)
4) \(\left(\frac{tanx-1}{tanx+1}+cot2x\right)\left(3tan-\sqrt{3}\right)=0;0< x< \pi\)
a/ ĐKXĐ: \(cos2x\ne0\)
\(\Leftrightarrow2x\ne\frac{\pi}{2}+k\pi\Rightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
Pt tương đương:
\(\left[{}\begin{matrix}sin\left(x-\frac{\pi}{4}\right)=0\\2cosx+\sqrt{2}=0\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{4}=k\pi\\cosx=cos\left(\frac{3\pi}{4}\right)\\2x=k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\left(l\right)\\x=\frac{3\pi}{4}+k2\pi\left(l\right)\\x=-\frac{3\pi}{4}+k2\pi\left(l\right)\\x=\frac{k\pi}{2}\end{matrix}\right.\) \(\Rightarrow x=\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
b/
ĐKXĐ: \(x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
\(\Leftrightarrow tan2x.sinx+3sinx-\sqrt{3}tan2x-3\sqrt{3}=0\)
\(\Leftrightarrow sinx\left(tan2x+3\right)-\sqrt{3}\left(tan2x+3\right)=0\)
\(\Leftrightarrow\left(sinx-\sqrt{3}\right)\left(tan2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=\sqrt{3}>1\left(vn\right)\\tan2x=-3\end{matrix}\right.\)
\(\Rightarrow2x=arctan\left(-3\right)+k\pi\)
\(\Rightarrow x=\frac{arctan\left(-2\right)}{2}+\frac{k\pi}{2}\)
Đúng 0
Bình luận (0)
c/
ĐKXĐ: \(\left\{{}\begin{matrix}sin\left(x+\frac{3\pi}{4}\right)\ne0\\cos2x\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x+\frac{3\pi}{4}\ne k\pi\\2x\ne\frac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne-\frac{3\pi}{4}+k\pi\\x\ne\frac{\pi}{4}+\frac{k\pi}{2}\end{matrix}\right.\) \(\Rightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\)
Pt tương đương:
\(cos^22x=sin^2\left(x+\frac{3\pi}{4}\right)\)
\(\Leftrightarrow\frac{1}{2}+\frac{1}{2}cos4x=\frac{1}{2}-\frac{1}{2}cos\left(2x+\frac{3\pi}{2}\right)\)
\(\Leftrightarrow cos4x=-cos\left(2x+\frac{3\pi}{2}\right)=cos\left(2x+\frac{\pi}{2}\right)\)
\(\Rightarrow\left[{}\begin{matrix}4x=2x+\frac{\pi}{2}+k2\pi\\4x=-2x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\left(l\right)\\x=-\frac{\pi}{12}+\frac{k\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải pt: 3tan2x+\(\frac{3\left(tanx+1\right)}{Cosx}\)=1+\(4\sqrt{2}sin\left(x-\frac{15\pi}{4}\right)\)
ĐKXĐ: \(x\ne\frac{\pi}{2}+k\pi\)
\(\frac{3sin^2x}{cos^2x}+\frac{3\left(sinx+cosx\right)}{cos^2x}=1+4\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\frac{3sin^2x}{cos^2x}+\frac{3\left(sinx+cosx\right)}{cos^2x}=1+4\left(sinx+cosx\right)\)
\(\Leftrightarrow\frac{3-3cos^2x}{cos^2x}-1+\frac{3\left(sinx+cosx\right)}{cos^2x}-4\left(sinx+cosx\right)=0\)
\(\Leftrightarrow\frac{3-4cos^2x}{cos^2x}+\left(sinx+cosx\right)\left(\frac{3-4cos^2x}{cos^2x}\right)=0\)
\(\Leftrightarrow\left(\frac{3-4cos^2x}{cos^2x}\right)\left(sinx+cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3-4cos^2x=0\\sinx+cosx=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^2x=\frac{3}{4}\\\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=-1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{\sqrt{3}}{2}\\cosx=\frac{-\sqrt{3}}{2}\\sin\left(x+\frac{\pi}{4}\right)=\frac{-\sqrt{2}}{2}\end{matrix}\right.\) \(\Rightarrow...\)
Đúng 0
Bình luận (0)
Giải phương trình 3tan2x + 4sin2x - 2
3
tanx - 4sinx + 2 0 A. x ±
π
6
+ k2π, k ∈ Z B. x
π
6
+ kπ, k ∈ Z C. x
-
π
4
+ k2π,
-
π
6
+ k2π, k ∈ Z D. Tất cả sai
Đọc tiếp
Giải phương trình 3tan2x + 4sin2x - 2 3 tanx - 4sinx + 2 = 0
A. x = ± π 6 + k2π, k ∈ Z
B. x = π 6 + kπ, k ∈ Z
C. x = - π 4 + k2π, - π 6 + k2π, k ∈ Z
D. Tất cả sai
Giải pt:
\(sin^3x-cos^3x+3sin^2x+4sinx-cosx+2=0\)
\(\Leftrightarrow sin^3x+3sin^2x+3sinx+1-cos^3x+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx+1\right)^3-cos^3x+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx-cosx+1\right)\left[\left(sinx+1\right)^2+cosx\left(sinx+1\right)+cos^2x\right]+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx-cosx+1\right)\left(2sinx+sinx.cosx+cosx+2\right)+sinx-cosx+1=0\)
\(\Leftrightarrow\left(sinx-cosx+1\right)\left(2sinx+cosx+sinx.cosx+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=-1\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\Leftrightarrow...\\2sinx+cosx+sinx.cosx+3=0\left(1\right)\end{matrix}\right.\)
Xét (1):
\(\Leftrightarrow2\left(sinx+1\right)+cosx\left(sinx+1\right)+1=0\)
\(\Leftrightarrow\left(cosx+2\right)\left(sinx+1\right)+1=0\)
Do \(sinx;cosx\ge-1\Rightarrow\left(cosx+2\right)\left(sinx+1\right)\ge0\)
\(\Rightarrow\left(cosx+2\right)\left(sinx+1\right)+1=0\) vô nghiệm
đây là toán lớp 10 mọi người giải giúp em với,em đang ôn chuẩn bị thi nhưng bài này chưa biết làm
tanx - sinx/sin^3x=1/cox(1 + cosx)
sinx . sin (pi/3 - x) . sin(pi/3 + x)=1/4sin3x
giai cac pt
a) \(sin^3\left(x+\frac{\pi}{4}\right)=\sqrt{2}sinx\)
b) \(cos^3x-sin^3x=\sqrt{2}cos\left(x-\frac{\pi}{4}\right)\)
c) \(\frac{1-tanx}{1+tanx}=1+2sinx\)
d) \(\left(1+tanx\right)sin^2x=3sinx\left(cosx-sinx\right)+3\)