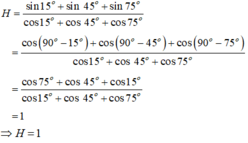chứng minh rằng \(\sin75\)

Những câu hỏi liên quan
Chứng minh rằng \(\sin75^o=\frac{\sqrt{6}+\sqrt{2}}{4}\)
Chứng minh rằng :
a) \(\sin105^0=\sin75^0\)
b) \(\cos170^0=-\cos10^0\)
c) \(\cos122^0=-\cos58^0\)
a) Ta có: sin 1050 = sin(1800-1050) => sin 1050= sin 750
b) cos1700= -cos(1800-1700) => cos1700 = -cos100
c) cos1220 = -cos(1800-1220) => cos1220 = -cos580
Đúng 0
Bình luận (0)
Chứng minh rằng :
a) sin1050 = sin750; b) cos1700 = -cos100 c) cos1220 = -cos580
a) Ta có: sin 1050 = sin(1800-1050) => sin 1050= sin 750
b) cos1700= -cos(1800-1700) => cos1700 = -cos100
c) cos1220 = -cos(1800-1220) => cos1220 = -cos580
Đúng 0
Bình luận (0)
Tính \(\sin75\)
\(sin75=\frac{\sqrt{6}+\sqrt{2}}{4}\)
nhớ k đấy
Đúng 0
Bình luận (0)
\(\sin75=\frac{\sqrt{6}+\sqrt{2}}{9}\)
Lấy mấy tính mà tính chứ ko biết cách làm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giá trị của biểu thức sau là:
H
sin
15
°
+
sin
45
°
+
sin
75
°
cos
15
°
+
cos
45
°
+
cos...
Đọc tiếp
Giá trị của biểu thức sau là:
H = sin 15 ° + sin 45 ° + sin 75 ° cos 15 ° + cos 45 ° + cos 75 °
A. H = 1
B. H = -1
C. H = 0
D. H = 1/2
Chứng minh:
\(\sin75\)= \(\frac{\sqrt{6}+\sqrt{2}}{4}\)
\(\cos75\)= \(\frac{\sqrt{6}-\sqrt{2}}{4}\)
\(\sin15\)= \(\frac{\sqrt{6}+2}{2}\)
\(\tan15\)= \(2-\sqrt{3}\)
Tính giá trị biểu thức sau:
\(\sin15^0+\sin75^0-\cos15^0-\cos75^0+\sin30^0\)
\(sin15^o+sin75^o-cos15^o-cos75^o+sin30^o\)
\(=\left(sin15+sin75^o\right)-\left(cos15^o+cos75^o\right)+sin30^o\)
\(=\dfrac{\sqrt{6}}{2}-\dfrac{\sqrt{6}}{2}+\dfrac{1}{2}\)
\(=0+\dfrac{1}{2}\)
\(=\dfrac{1}{2}\)
Đúng 3
Bình luận (0)
\(sin15^o+sin75^o-cos15^0-cos75^o+sin30^o\)
\(=cos75^o+cos15^0-cos15^0-cos75^o+sin30^o\)
\(=sin30^o=\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
không dùng bảng số hoặc máy tính.C/m
\(sin75^o=\frac{\sqrt{6}+\sqrt{2}}{4}\)
Tính giá trị biểu thức:
A= \(\sin15^0+\sin75^0-\cos15^0-\cos75^0+\sin30^0\)
A=sin 150+sin 750-sin 750-sin 150+sin 300
A=sin 300=\(\dfrac{1}{2}\)=0,5
vì cos 150=sin (900-150)=sin 750
cos 750=sin (900-750)=sin 150
Đúng 0
Bình luận (1)