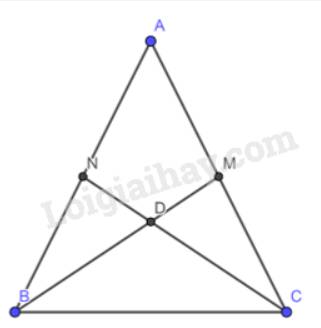
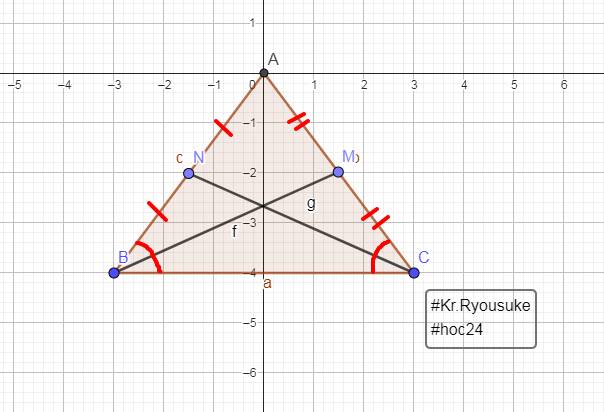
Cho tam giác ABC. Trung tuyến BM; CN. Lấy E thuộc tia BM sao cho M là trung điểm BE.
a) C/minh AE//BC.
b) Lấy F thuộc tia CN sao cho N là trung điểm của CF. C/minh BC//EF.
c) Gọi giao điểm của EN và AC là K. C/minh CK=2AK.
Giúp mình câu c gấp với nhé (câu a,b k cần)