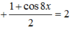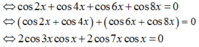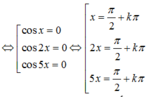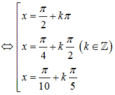cos23x*cos2x-cos2x=0

Những câu hỏi liên quan
Giải các phương trình cos 2 x + cos 2 2 x - cos 2 3 x - cos 2 4 x = 0
Tìm các họ nghiệm của phương trình
cos
2
x
+
cos
2
2
x
+
cos
2
3
x
+
cos
2
4
x
2
A.
x...
Đọc tiếp
Tìm các họ nghiệm của phương trình cos 2 x + cos 2 2 x + cos 2 3 x + cos 2 4 x = 2
A. x = π 2 + k π x = π 4 + k π 2 x = π 10 + k π 5
B. x = - π 2 + k π x = π 4 + k π 2 x = π 10 + k π 5
C. x = π 2 + k π x = - π 4 + k π 2 x = π 10 + k π 5
D. x = π 2 + k π x = π 4 + k π 2 x = - π 10 + k π 5
Phương trình đã cho tương đương với:
1 + cos 2 x 2 + 1 + cos 4 x 2 + 1 + cos 6 x 2 + 1 + cos 8 x 2 = 2 ⇔ cos 2 x + cos 4 x + cos 6 x + cos 8 x = 0 ⇔ cos 2 x + cos 4 x + cos 6 x + cos 8 x = 0 ⇔ 2 cos 3 x cos x + 2 cos 7 x cos x = 0 ⇔ 2 cos x cos 3 x + cos 7 x = 0 ⇔ 4 cos x cos 2 x cos 5 x = 0 ⇔ cos x = 0 cos 2 x = 0 cos 5 x = 0 ⇔ x = π 2 + k π x = π 4 + k π 2 x = π 10 + k π 5
Đáp án A
Đúng 0
Bình luận (0)
Tìm các họ nghiệm của phương trình
cos
2
x
+
cos
2
2
x
+
cos
2
3
x
+
cos
2
4
x
2
Đọc tiếp
Tìm các họ nghiệm của phương trình cos 2 x + cos 2 2 x + cos 2 3 x + cos 2 4 x = 2
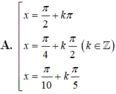
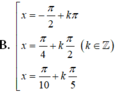
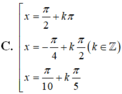
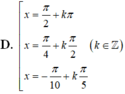
Chọn A
Phương trình đã cho tương đương với:
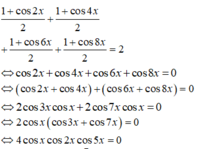
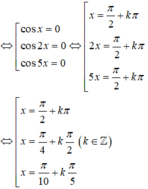
Đúng 0
Bình luận (0)
Tìm các họ nghiệm của phương trình
cos
2
x
+
cos
2
2
x
+
cos
2
3
x
+
cos
2
4
x
2
Đọc tiếp
Tìm các họ nghiệm của phương trình
cos 2 x + cos 2 2 x + cos 2 3 x + cos 2 4 x = 2
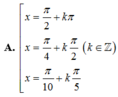
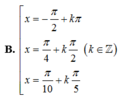
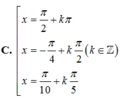
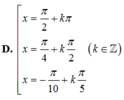
1+sinx-cos2x=0
Sin3x+cos2x-sinx=0
\(1+sinx-cos2x=0\)
\(\Leftrightarrow1+sinx-\left(1-2sin^2x\right)=0\)
\(\Leftrightarrow sinx\left(1+2sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=-\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(sin3x-sinx+cos2x=0\)
\(\Leftrightarrow2cos2x.sinx+cos2x=0\)
\(\Leftrightarrow cos2x\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sinx=-\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=-\frac{\pi}{6}+k2\pi\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
giải phương trình
1. sin2x+3sinx-cos2x=-2
2. sin2x+sinx-cos2x=0
`1)sin^2 x+3sin x-cos^2 x=-2`
`<=>sin^2 x+3sin x-1+sin^2 x+2=0`
`<=>2sin^2 x+3sin x+1=0`
`<=>[(sin x=-1),(sin x=-1/2):}`
`<=>[(x=-\pi/2 +k2\pi),(x=-\pi/6 +k2\pi),(x=[7\pi]/6+k2\pi):}` `(k in ZZ)`
`2)sin^2 x+sin x-cos^2 x=0`
`<=>sin^2 x+sin x-1+sin^2 x=0`
`<=>2sin^2 x+sin x-1=0`
`<=>[(sin x=-1),(sin x=1/2):}`
`<=>[(x=-\pi/2 +k2\pi),(x=\pi/6 +k2\pi),(x=[5\pi]/6 +k2\pi):}` `(k in ZZ)`
Đúng 2
Bình luận (0)
Tập nghiệm của phương trình cos 2 x – cos 2 x = 0 trong khoảng [0;2π) là:
A. {0;π}
B. {0;π/2}
C. {π/2; 3π/2}
D. {0; 3π/2}
Chọn A
cos 2 x − cos 2 x = 0 ⇔ cos 2 x − ( cos 2 x − sin 2 x ) = 0 ⇔ sin 2 x = 0 ⇔ sin x = 0 ⇔ sin x = k π ; k ∈ Z
Tập nghiệm của phương trình cos 2 x – cos 2 x = 0 trong khoảng [0,2π) là 0 ; π
Đúng 0
Bình luận (0)
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
Đúng 0
Bình luận (0)
Giải phương trình
1,sin3x+cos2x=1+2sinx*cos2x
2,cos5x+cos2x+2sin3x*sin2x=0
a, cos3x + cos2x - cosx - 1 = 0
b, cos(8sinx) = 1
c, 1 + cos2x + cosx = 0
d, 3cosx + |sinx| = 2
a/
\(\Leftrightarrow4cos^3x-3cosx+2cos^2x-1-cosx-1=0\)
\(\Leftrightarrow2cos^3x+cos^2x-2cosx-1=0\)
\(\Leftrightarrow cos^2x\left(2cosx+1\right)-\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left(cos^2x-1\right)\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\2cosx+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b/
\(cos\left(8sinx\right)=1\)
\(\Leftrightarrow8sinx=k2\pi\)
\(\Leftrightarrow sinx=\frac{k\pi}{4}\)
Do \(-1\le sinx\le1\Rightarrow-1\le\frac{k\pi}{4}\le1\)
\(\Rightarrow k=\left\{-1;0;1\right\}\)
\(\Rightarrow\left[{}\begin{matrix}sinx=-\frac{\pi}{4}\\sinx=0\\sinx=\frac{\pi}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm arcsin\left(\frac{\pi}{4}\right)+k2\pi\\x=\pi\pm arcsin\left(\frac{\pi}{4}\right)+k2\pi\\x=k\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
c/
\(\Leftrightarrow1+2cos^2x-1+cosx=0\)
\(\Leftrightarrow2cos^2x-cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\pm\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
d/
Đặt \(\left\{{}\begin{matrix}\left|sinx\right|=a\ge0\\cosx=b\end{matrix}\right.\) ta được hệ:
\(\left\{{}\begin{matrix}a+3b=2\\a^2+b^2=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2-3b\\a^2+b^2=1\end{matrix}\right.\)
\(\Rightarrow\left(2-3b\right)^2+b^2-1=0\)
\(\Rightarrow10b^2-12b+3=0\Rightarrow\left[{}\begin{matrix}b=\frac{6+\sqrt{6}}{10}\Rightarrow a=\frac{2-3\sqrt{6}}{10}\left(l\right)\\b=\frac{6-\sqrt{6}}{10}\Rightarrow a=\frac{2+3\sqrt{6}}{10}\end{matrix}\right.\)
\(\Rightarrow cosx=\frac{6-\sqrt{6}}{10}\)
\(\Rightarrow x=\pm arccos\left(\frac{6-\sqrt{6}}{10}\right)+k2\pi\)
Đúng 0
Bình luận (0)