ĐKXĐ: \(m\ne-\dfrac{1}{3}\)

a) Để (P) đi qua điểm \(E\left(\dfrac{1}{2};\dfrac{1}{4}\right)\) thì

Thay \(x=\dfrac{1}{2}\)và \(y=\dfrac{1}{4}\) vào hàm số \(y=\left(3m+1\right)x^2\), ta được:

\(\left(3m+1\right)\cdot\dfrac{1}{4}=\dfrac{1}{4}\)

\(\Leftrightarrow3m+1=1\)

\(\Leftrightarrow3m=0\)

hay m=0(thỏa ĐK)

b) Ta có: \(\left\{{}\begin{matrix}3x-4y=2\\-4x+3y=-5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}12x-16y=8\\-12x+9y=-15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7y=-7\\3x-4y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\3x=2+4y=2+4=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

Vậy: F(2;1)

Để (P) đi qua điểm F(2;1) thì 

Thay x=2 và y=1 vào hàm số \(y=\left(3m+1\right)x^2\), ta được:

\(\left(3m+1\right)\cdot4=1\)

\(\Leftrightarrow3m+1=\dfrac{1}{4}\)

\(\Leftrightarrow3m=-\dfrac{3}{4}\)

\(\Leftrightarrow m=\dfrac{-3}{4}:3=\dfrac{-3}{4}\cdot\dfrac{1}{3}=\dfrac{-1}{4}\)(thỏa ĐK)

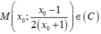- Gọi với  là điểm cần tìm.

- Gọi  ∆ tiếp tuyến của (C)  tại M ta có phương trình.

- Gọi 

- Khi đó ∆ tạo với hai trục tọa độ tam  giác OAB  có trọng tâm là

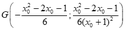
- Do G  thuộc đường thẳng  4x+y=0 nên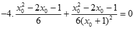 

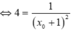(vì A; B không trùng O nên   ) 

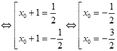
- Vì x₀>-1 nên chỉ chọn 

Chọn A.

a) \(\hept{\begin{cases}x=1\\y=3\end{cases}\Rightarrow3=a.1\Rightarrow a=3}\)

b) B(x_o,y_o) thuộc y=3x=> y_o=3.x_o

_{\(p=\frac{x_o+1}{3x_o+3}=\frac{x_o+1}{3\left(x_o+1\right)}\)} 

\(\hept{\begin{cases}x_0=-1\Rightarrow P=kXD\\x_o\ne-1\Rightarrow P=\frac{1}{3}\end{cases}}\)

??????????

Đáp án D

Giao điểm của hai đường tiệm cận là I ( -1;2 )

y = 2 x - 1 x + 1   ⇒ y ' = 3 x + 1 2   ⇒ PTTT tại  M x 0 , y 0 là

( d )   y = 3 x 0 + 1 2 x - x 0 + 2 x 0 - 1 x 0 + 1

Giao của (d) với TCD x = -1 là A - 1 ; 2 x 0 - 4 x 0 - 1 , Giao của (d) với TCD B 2 x 0 + 1 ; 2

A B 2 + I B 2 = 40   ⇔ 2 - 2 x 0 - 4 x 0 - 1 2 + - 2 x 0 - 2 2 = 40

⇔ 36 x 0 + 1 2 + 4 x 0 + 1 2 = 40

x 0 + 1 4 - 10 x 0 + 1 2 + 9 = 0 ⇔ x 0 + 1 2 = 1 x 0 + 1 2 = 9 ⇒ x 0 = 2 x 0 > 0 ⇒ y 0 = - 1 ⇒ x 0 y 0 = 2

Đáp án cần chọn là D