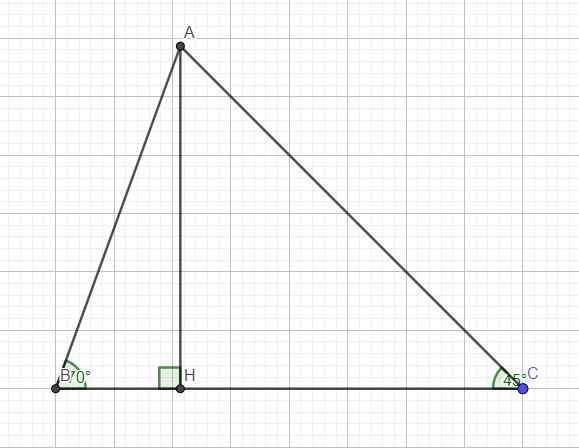
\(\Delta ABC\) có \(\widehat{A}=105^0,\widehat{B}=45^0,BC=4cm\) . Tính độ dài cạnh AB, AC.

Những câu hỏi liên quan
Tam giác ABC có \(\widehat{A}=105^0;\widehat{B}=45^0;CB=4cm\). Tính độ dài các cạnh AB, AC ?
\(\Delta ABC\) có \(\widehat{A}=105^0\) , \(\widehat{B}=45^0,BC=4cm\) . Tính độ dài cạnh AB và AC
Tam giác ABC có \(\widehat{B}=60^0;\widehat{C}=45^0;BC=a\). Tính độ dài hai cạnh AB và AC ?
Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{A}=75^o\)
* \(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\Rightarrow AB=\dfrac{BCsinC}{sinA}=a\left(1+\sqrt{3}\right)\)
* \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{BCsinB}{sinA}=a\left(\dfrac{-6+3\sqrt{2}}{2}\right)\)
Đúng 0
Bình luận (0)
\(\Delta ABC\) có \(\widehat{B}=60^0,BC=8cm,AB+AC=12cm\) .Tính độ dài cạnh AC.
\(\Delta ABC\) có \(\widehat{A}=60^0,AB=28cm,AC=35cm\) .Tính độ dài cạnh BC.
Vẽ BH vuông góc với AC
Theo định lý Pythagore, ta có:
BC2=BH2+CH2=BH2+(AC-AH)2
=BH2+AH2+AC2-2AC.AH
Mà ta lại có:AH2+BH2=AB2 (định lý Pythagore, tam giác ABH vuông tại H)
và AH=1/2AB (do tam giác ABH là nửa tam giác đều)
Cho nên: BC2=AB2+AC2-2.1/2AB.AC=AB2+AC2-AB.AC (*)
Thay AB=28cm, AC=35cm vào (*), ta được:
BC2=1029=>BC=7\(\sqrt{21}\)cm
Vậy BC=7\(\sqrt{21}\)cm
Đúng 0
Bình luận (0)
Tam giác ABC có ∠ A = 105 ° , ∠ B= 45 ° , BC = 4cm. Tính độ dài các cạnh AB, AC.
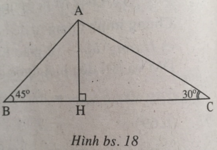
Vẽ đường cao AH. Đặt BH = x, CH = y thì do H nằm giữa B và C (hai góc ∠ B, ∠ C là góc nhọn) suy ra x + y = 4 (xem h.bs.18).
Ta có BH = AH = HC.tg 30 ° nên x – y.tg 30 ° = y/ 3
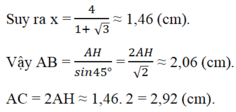
AC = 2AH ≈ 1,46. 2 = 2,92 (cm).
Đúng 0
Bình luận (0)
Bài 1 Cho tam giác ABC,BC=4,\(\widehat{B}\)=450,\(\widehat{A}\)=1050.Tính AB và BC
Bài 2 Cho tam giác ABC,AB=28cm,AC=35cm,\(\widehat{A}\)=60.Tính BC
Bài 2:
\(\cos60^0=\dfrac{28^2+35^2-BC^2}{2\cdot28\cdot35}\)
\(\Leftrightarrow2009-BC^2=980\)
hay \(BC=7\sqrt{21}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = 4cm, \(\widehat{B}=70^o\), \(\widehat{C}=45^o\). Tính độ dài AC và diện tích tam giác ABC?
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Tam giác ABC có ˆA=105∘A^=105∘, ˆB=45∘B^=45∘, BC = 4cm. Tính độ dài các cạnh AB, AC.
Vẽ đường cao AH . Đặt BH = x, CH = y thì do H nằm giữa B và C ( hai góc \(\widehat{B } ; \widehat{C}\) là góc nhọn) suy ra x + y = 4
Ta có \(BH=AH=HC.tg30^o\)nên \(x-y.tg30^o=y\sqrt{3}\)
\(\Rightarrow x=\frac{4}{1+\sqrt{3}}\approx1,46\left(cm\right)\)
Vậy \(AB=\frac{AH}{\sin45^o}=\frac{2AH}{\sqrt{2}}\approx2,06\left(cm\right)\)
\(AC=2AH\approx1,46.2=2,92\left(cm\right)\)
AC = 2AH ≈ 1,46. 2 = 2,92 ( cm )