Ôn tập Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
Cho tam giác ABC vuông tại C có \(\widehat{B}=37^0\). Gọi I là giao điểm của cạnh BC với đường trung trực của AB. Hãy tính AB, AC nếu biết BI = 20
Cho Delta ABC vuông tại B có widehat{C}60^0,AC 6 cma) Trên tia đối của tia CB lấy điểm N sao cho CN AC. C/m dfrac{CB}{CN}dfrac{AB}{AN}b) Đường thẳng song song với đường phân giác của widehat{ACN} kẻ từ B cắt AN tại H. C/m dfrac{1}{BH^2}dfrac{1}{AB^2}+dfrac{1}{BN^2}
Đọc tiếp
Cho \(\Delta ABC\) vuông tại B có \(\widehat{C}=60^0\),AC = 6 cm
a) Trên tia đối của tia CB lấy điểm N sao cho CN = AC. C/m \(\dfrac{CB}{CN}=\dfrac{AB}{AN}\)
b) Đường thẳng song song với đường phân giác của \(\widehat{ACN}\) kẻ từ B cắt AN tại H. C/m \(\dfrac{1}{BH^2}=\dfrac{1}{AB^2}+\dfrac{1}{BN^2}\)
20 tháng 7 2023 lúc 22:11
Cho tam giác ABC vuông tại B. Giải tam giác ABC, biết rằng:
a) \(\widehat{A}\) = \(40^0\), AC = 8cm
b) cotC = \(\dfrac{1}{\sqrt{3}}\); AB = 5cm
24 tháng 7 2023 lúc 7:54
Cho tam giác ABC vuông tại A có \(\widehat{B}\) = \(60^0\), BC = 6cm.
a) Tính AB, AC (kết quả làm tròn đến chữ số thập phân thứ nhất)
b) Kẻ đường cao AH của tam giác ABC. Tính HB, HC
c) Trên tia đối của tia BA lấy điểm D sao cho DB = BC. Chứng minh: \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm, BC = 7,5 cm
a) Chứng minh tam giác ABC vuông tại A. Tính các góc \(\widehat{B},\widehat{C}\) và đường cao AH của tam giác
b) Tìm tập hợp các điểm M sao cho \(S_{ABC}=S_{BMC}\)
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm, BC = 7,5 cm
a) Chứng minh tam giác ABC vuông tại A. Tính các góc \(\widehat{B},\widehat{C}\) và đường cao AH của tam giác
b) Tìm tập hợp các điểm M sao cho \(S_{ABC}=S_{BMC}\)
Cho tam giác ABC vuông tại A có AB = 12 cm, acb = 50 độ 0 a) Tính độ dài BC và AC? b) Kẻ tia phân giác BD của góc ABC (D AC). Tính AD, DC, BD? (Kết quả về cạnh làm tròn đến chữ số thập phân thứ hai)
Tam giác ABC có \(\widehat{A}=20^0,\widehat{B}=30^0;AB=60cm\). Đường vuông góc kẻ từ C đến AB cắt AB tại P (h.33)
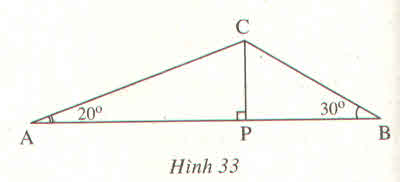
Hãy tìm :
a) AP, BP
b) CP
Cho hình thang ABCD. Biết hai đáy AB = a, CD = 2a, cạnh bên AD = a, \(\widehat{A}=90^0\)
a) Chứng minh tg C = 1
b) Tính tỉ số diện tích tam giác DBC và diện tích hình thang ABCD
c) Tính tỉ số diện tích tam giác ABC và diện tích tam giác DBC