Theo hệ thức lượng trong tam giác vuông ta có \(AB^2=BH.BC\Rightarrow3^2=\left(BC-HC\right).BC\Rightarrow BC^2-3,2.BC-9=0\)

\(\Leftrightarrow\orbr{\begin{cases}BC=5\\BC=-\frac{9}{5}\left(l\right)\end{cases}\Leftrightarrow BC=5\left(cm\right)}\)

Theo định lí PItago ta có \(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)

Ta có \(AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4\left(cm\right)\)

Xét tam giác ABH và tam giác AHC có:

góc H₁= góc H2(=90^o)

góc A₁= góc C₁(Phụ góc A₂)

\(\Rightarrow\)\(\Delta ABH\Omega\Delta AHC\left(g.g\right)\)

\(\Rightarrow\frac{AB}{AH}=\frac{AH}{HC}\Rightarrow AH^2=AB.HC=3.3,2=9,6\)

\(\Rightarrow AH=\sqrt{9,6}\approx3,1\left(cm\right)\)

Vây AH=3,1cm

\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)

BC=HB+HC=6,25(cm)

AM=BC/2=3,125(cm)

\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)

\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)

+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :

\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)

+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\) 

\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\) 

\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)

+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :

\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)

\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)

+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :

\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)

Xét tam giác ABH vuông tại H, ta có:

\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)

\(\Rightarrow AB=5\left(cm\right)\)

Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:

\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)

Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)

AM là đường trung tuyến trong tam giác vuông ABC

=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)

Bài 5: 

a) Xét ΔABC vuông tại A có 

\(AC=AB\cdot\cot\widehat{C}\)

\(=21\cdot\cot40^0\)

\(\simeq25,03\left(cm\right)\)

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)

hay \(BC\simeq32,67\left(cm\right)\)

+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:

+) Áp dụng hệ thức về cạnh và đường cao trng tam giác vuông ABC với AH là đường cao ta có:

+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:

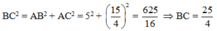
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có:

+) Diện tích tam giác ABC với AH là đường cao ta có:

Vậy AB = 5cm, AC =  15 4 cm; AM =  25 8 cm;     S ∆ A B C = 75 8 c m 2 .

Đáp án cần chọn là: A

Áp dụng HTL tam giác: 

\(\left\{{}\begin{matrix}AH^2=BH\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}HC=\dfrac{AH^2}{BH}=\dfrac{16}{3}\left(cm\right)\\AB^2=3\left(3+\dfrac{16}{3}\right)=25\left(cm\right)\\AC^2=\dfrac{16}{3}\left(3+\dfrac{16}{3}\right)=\dfrac{400}{9}\left(cm\right)\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}HC=\dfrac{16}{3}\left(cm\right)\\AB=5\left(cm\right)\\AC=\dfrac{20}{3}\left(cm\right)\end{matrix}\right.\)

\(BC=\sqrt{AB^2+AC^2}=\dfrac{25}{3}\left(cm\right)\left(pytago\right)\)

Xét tam giác ABH vuông tại H có:

\(AB^2=BH^2+AH^2\left(Pytago\right)\)

\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2^2}=\sqrt{5}\left(cm\right)\)

Áp dụng HTL trong tam giác ABC vg tại A có đg cao AH:

\(AH^2=BH.HC\)

\(\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{2^2}{\sqrt{5}}=\dfrac{4\sqrt{5}}{5}\left(cm\right)\)

Ta có: \(AC^2=HC^2+AH^2\left(Pytago\right)\)

\(\Rightarrow AC=\sqrt{AH^2+HC^2}=\sqrt[]{2^2+\left(\dfrac{4\sqrt{5}}{5}\right)^2}=\dfrac{6\sqrt{5}}{5}\left(cm\right)\)

Ta có: \(BC=HC+BH=\sqrt{5}+\dfrac{4\sqrt{5}}{5}=\dfrac{5+4\sqrt{5}}{5}\left(cm\right)\)