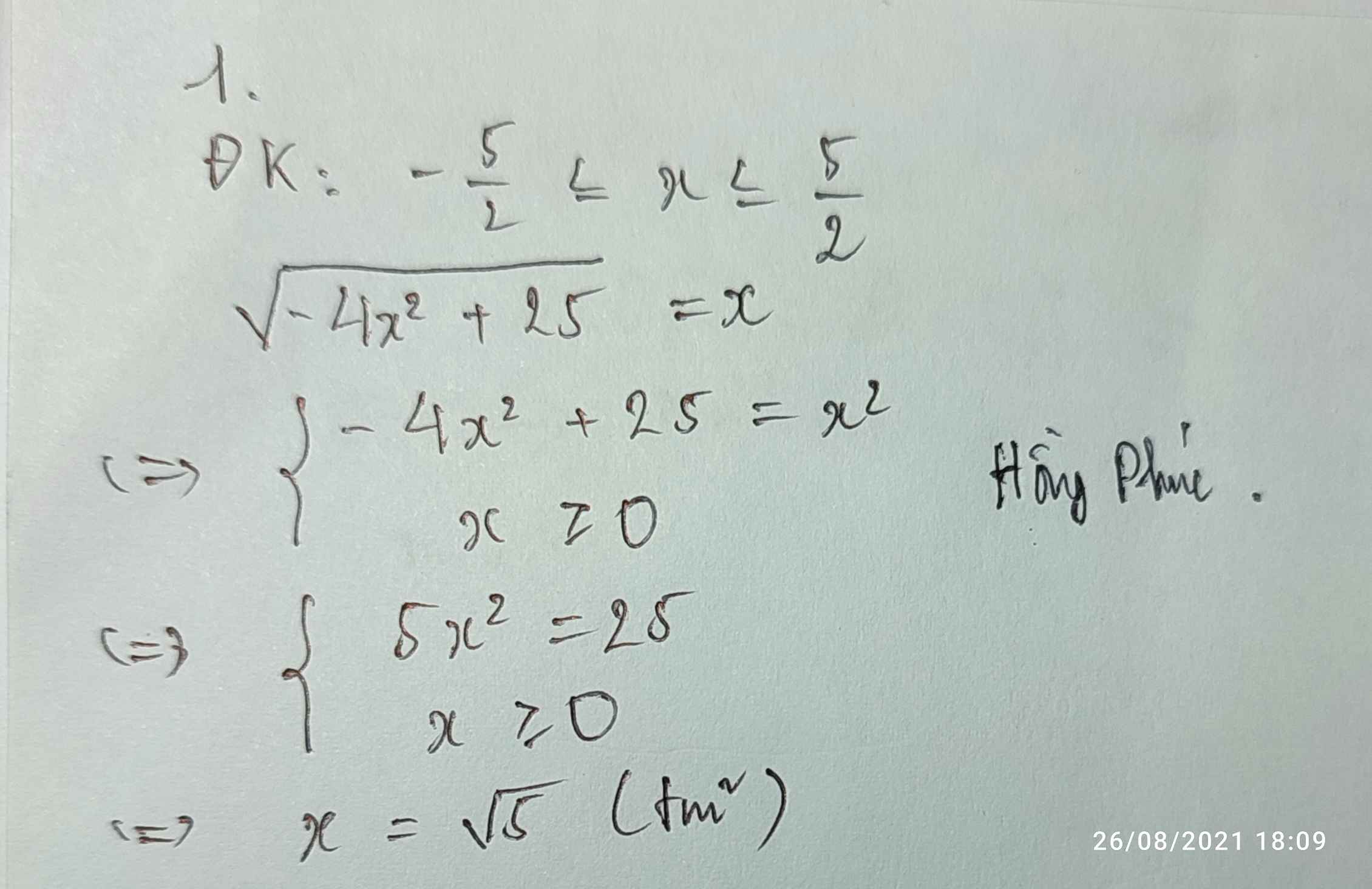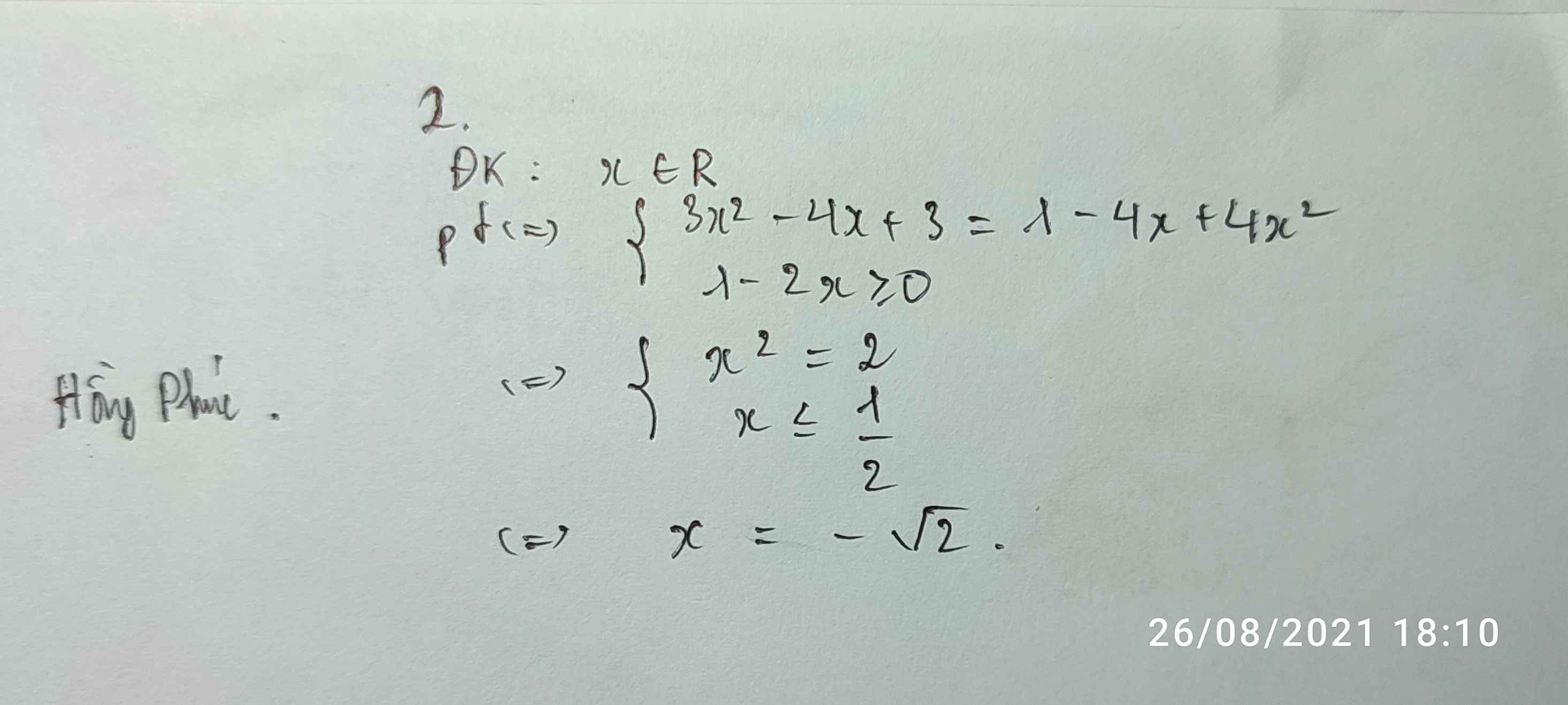\(N=\dfrac{5\sqrt{x}+3x}{x+2\sqrt{x}-3}-\dfrac{3\sqrt{x}-1}{1-\sqrt{x}}+\dfrac{7}{\sqrt{x}+3}\)

\(=\dfrac{5\sqrt{x}+3x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\dfrac{\left(3\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\dfrac{7\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{5\sqrt{x}+3x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\dfrac{3x+8\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\dfrac{7\sqrt{x}-7}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{20\sqrt{x}+6x-10}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)

Đề sai không vậy?

Ta có: \(N=\dfrac{3x+5\sqrt{x}}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{7}{\sqrt{x}+3}\)

\(=\dfrac{3x+5\sqrt{x}+3x+9\sqrt{x}-\sqrt{x}-3+7\sqrt{x}-7}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{6x+20\sqrt{x}-10}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)

a) \(D=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)

\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)

\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)

\(=\dfrac{-3\sqrt{x}+3}{\sqrt{x}+3}.\dfrac{1}{\sqrt{x}-1}=\dfrac{-3}{\sqrt{x}+3}\)

b) \(D=-\dfrac{3}{\sqrt{x}+3}< -\dfrac{1}{4}\)

\(\Leftrightarrow12>\sqrt{x}+3\Leftrightarrow\sqrt{x}< 9\) 

\(\Leftrightarrow0\le x< 81\) và \(x\ne9\)

a) D=\(\left(\dfrac{2\sqrt{x}.\left(\sqrt{x}-3\right)+\sqrt{x}.\left(\sqrt{x}+3\right)-3x-3}{\left(\sqrt{x}+3\right).\left(\sqrt{x}-3\right)}\right)\) \(:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)

\(\Leftrightarrow D=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}\) \(.\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)

\(\Leftrightarrow D=\dfrac{-3-3\sqrt{x}}{\sqrt{x}+3}.\dfrac{1}{\sqrt{x}+1}\)

\(\Leftrightarrow D=\dfrac{-3.\left(\sqrt{x}+1\right)}{\sqrt{x}+3}.\dfrac{1}{\sqrt{x}+1}\)

\(\Leftrightarrow D=\dfrac{-3}{\sqrt{x}+3}\)

b) Để D\(< \dfrac{-1}{4}\) \(\Leftrightarrow\dfrac{-3}{\sqrt{x}+3}< \dfrac{-1}{4}\) 

\(\Leftrightarrow12>\sqrt{x}+3\Leftrightarrow9>\sqrt{x}\Leftrightarrow81>x\ge0\)

Với x ≥ 0; x ≠ 9 ta có:

\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x-3}\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{3}{\sqrt{x}+3}\)

Vậy \(A=\dfrac{3}{\sqrt{x}+3}\).

\(P=\dfrac{x-5\sqrt{x}+2x+10\sqrt{x}-3x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}=\dfrac{5\sqrt{x}-25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}=\dfrac{5}{\sqrt{x}+5}\)

\(P=\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{2\sqrt{x}}{\sqrt{x}-5}-\dfrac{3x+25}{x-25}\\ \Leftrightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}-\dfrac{3x+25}{\left(\sqrt{x}+5\right)}\\ \Leftrightarrow P=\dfrac{x-5\sqrt{x}+2x+10\sqrt{x}-3x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\\ \Leftrightarrow P=\dfrac{5\sqrt{x}-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\\ \Leftrightarrow P=\dfrac{5\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)

\(\Leftrightarrow P=\dfrac{5}{\sqrt{x}+5}\)

-> \(\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}-\dfrac{3x+25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)

-> \(\dfrac{x-5\sqrt{x}+2x+10\sqrt{x}-3x-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)

-> \(\dfrac{5\sqrt{x}-25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)

-> \(\dfrac{5\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)

-> \(\dfrac{5}{\left(\sqrt{x}+5\right)}\)

a) Ta có: \(A=3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+30\)

\(=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+30\)

\(=14\sqrt{2x}+30\)

b) Ta có: \(B=4\sqrt{\dfrac{25x}{4}}-\dfrac{8}{3}\sqrt{\dfrac{9x}{4}}-\dfrac{4}{3x}\cdot\sqrt{\dfrac{9x^3}{64}}\)

\(=4\cdot\dfrac{5\sqrt{x}}{2}-\dfrac{8}{3}\cdot\dfrac{3\sqrt{x}}{2}-\dfrac{4}{3x}\cdot\dfrac{3x\sqrt{x}}{8}\)

\(=10\sqrt{x}-4\sqrt{x}-\dfrac{1}{2}\sqrt{x}\)

\(=\dfrac{11}{2}\sqrt{x}\)

c) Ta có: \(\dfrac{y}{2}+\dfrac{3}{4}\sqrt{9y^2-6y+1}-\dfrac{3}{2}\)

\(=\dfrac{1}{2}y+\dfrac{3}{4}\left(1-3y\right)-\dfrac{3}{2}\)

\(=\dfrac{1}{2}y+\dfrac{3}{4}-\dfrac{9}{4}y-\dfrac{3}{2}\)

\(=-\dfrac{7}{4}y-\dfrac{3}{4}\)

a: \(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{x-9}\cdot\dfrac{\sqrt{x}-7+\sqrt{x}+1}{\sqrt{x}+1}\)

\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{x-9}\cdot\dfrac{2\sqrt{x}-6}{\sqrt{x}+1}\)

\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+1}\cdot\dfrac{2}{\sqrt{x}+3}=-\dfrac{6}{\sqrt{x}+3}\)

b: P>=-1/2

=>P+1/2>=0

=>\(\dfrac{-6}{\sqrt{x}+3}+\dfrac{1}{2}>=0\)

=>\(\dfrac{-12+\sqrt{x}+3}{2\left(\sqrt{x}+3\right)}>=0\)

=>căn x-9>=0

=>x>=81

c: căn x+3>=3

=>6/căn x+3<=6/3=2

=>-6/căn x+3>=-2

Dấu = xảy ra khi x=0

1: ĐKXĐ: 3x^2-x+2>=0

=>x thuộc R

2: ĐKXĐ: x>=0 và căn x-1<>0 và 2-căn x<>0 và 2x+1>0 và x<>0

=>x>0 và x<>1 và x<>4