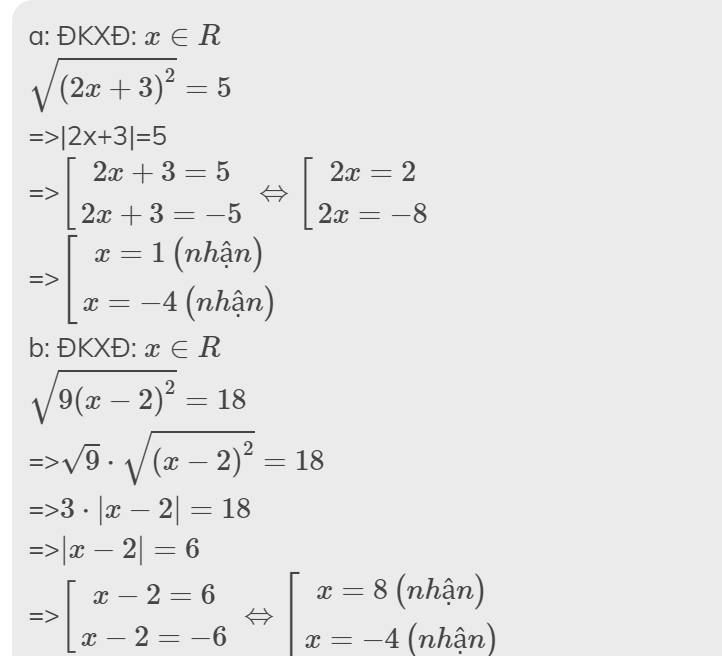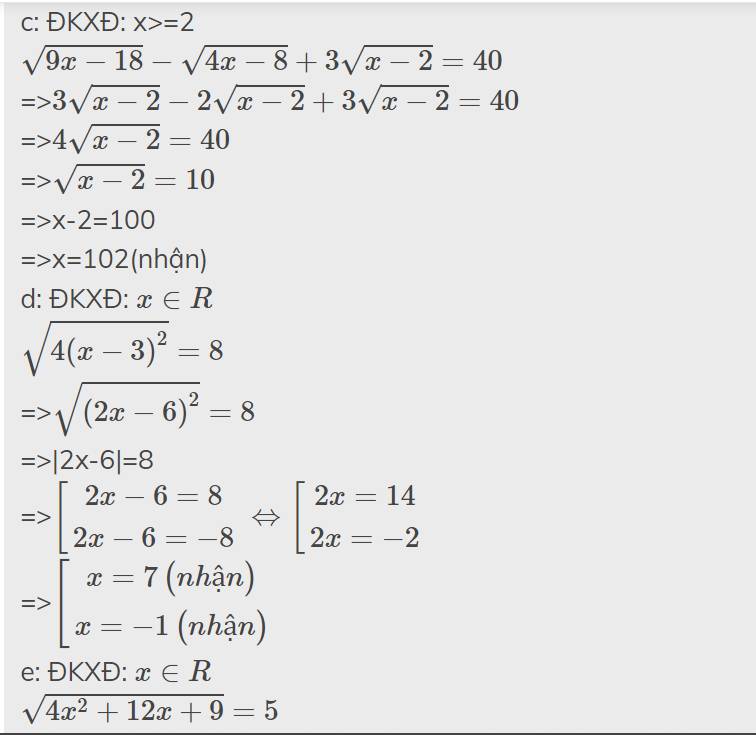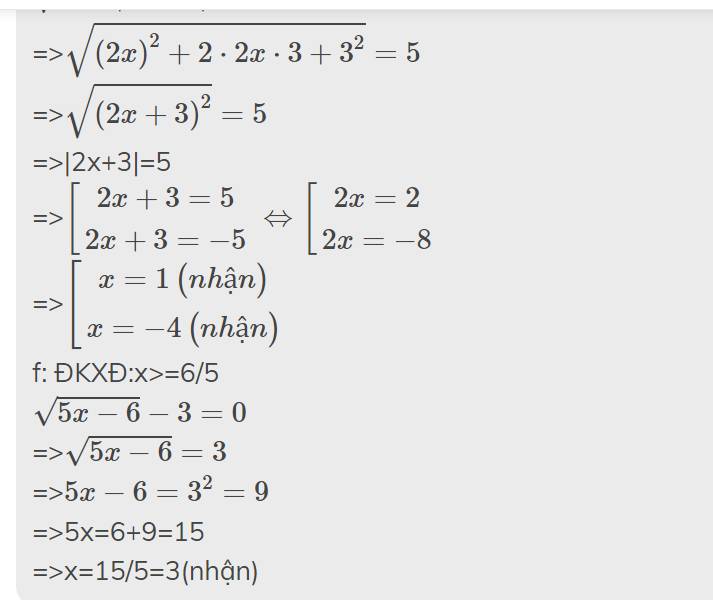Giải phương trình \(x^2-5x+4-\sqrt{5-x}-\sqrt{x-2}=0\)

Những câu hỏi liên quan
Giải các phương trình và hệ phương trình sau :
1. \(3x^2-7x+2=0\)
2. \(x^4-5x+4=0\)
3. \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\x-\sqrt{5}y=2\sqrt{5}\end{matrix}\right.\)
1. 3x( x - 2 ) - ( x - 2 ) = 0
<=> ( x-2).(3x-1) = 0 => x = 2 hoặc x = \(\dfrac{1}{3}\)
2. x( x-1 ) ( x2 + x + 1 ) - 4( x - 1 )
<=> ( x - 1 ).( x (x^2 + x + 1 ) - 4 ) = 0
(phần này tui giải được x = 1 thôi còn bên kia giải ko ra nha )
3 \(\left\{{}\begin{matrix}\sqrt{5}x-2y=7\\\sqrt{5}x-5y=10\end{matrix}\right.\)<=> \(\left\{{}\begin{matrix}y=-1\\x=\sqrt{5}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(1. 3x^2 - 7x +2=0\)
=>\(Δ=(-7)^2 - 4.3.2\)
\(= 49-24 = 25\)
Vì 25>0 suy ra phương trình có 2 nghiệm phân biệt:
\(x_1\)=\(\dfrac{-\left(-7\right)+\sqrt{25}}{2.3}=\dfrac{7+5}{6}=2\)
\(x_2\)=\(\dfrac{-\left(-7\right)-\sqrt{25}}{2.3}=\dfrac{7-5}{6}=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Giải bất phương trình sau : a/ 2x ^ 2 + 6x - 8 < 0 x ^ 2 + 5x + 4 >=\ 2) Giải phương trình sau : a/ sqrt(2x ^ 2 - 4x - 2) = sqrt(x ^ 2 - x - 2) c/ sqrt(2x ^ 2 - 4x + 2) = sqrt(x ^ 2 - x - 3) b/ x ^ 2 + 5x + 4 < 0 d/ 2x ^ 2 + 6x - 8 > 0 b/ sqrt(- x ^ 2 - 5x + 2) = sqrt(x ^ 2 - 2x - 3) d/ sqrt(- x ^ 2 + 6x - 4) = sqrt(x ^ 2 - 2x - 7)
2:
a: =>2x^2-4x-2=x^2-x-2
=>x^2-3x=0
=>x=0(loại) hoặc x=3
b: =>(x+1)(x+4)<0
=>-4<x<-1
d: =>x^2-2x-7=-x^2+6x-4
=>2x^2-8x-3=0
=>\(x=\dfrac{4\pm\sqrt{22}}{2}\)
Đúng 0
Bình luận (0)
Giải các phương trình sau:1) sqrt{3x^2+5x+8}-sqrt{3x^2+5x+1}12) x^2-2x-12+4sqrt{left(4-xright)left(2+xright)}03) 3sqrt{x}+dfrac{3}{2sqrt{x}}2x+dfrac{1}{2x}-74) sqrt{x}-dfrac{4}{sqrt{x+2}}+sqrt{x+2}05)left(x-7right)sqrt{dfrac{x+3}{x-7}}x+46) 2sqrt{x-4}+sqrt{x-1}sqrt{2x-3}+sqrt{4x-16}7) sqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}dfrac{x+3}{2}Giúp mình với ajk, mink đang cần gấp
Đọc tiếp
Giải các phương trình sau:
1) \(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
2) \(x^2-2x-12+4\sqrt{\left(4-x\right)\left(2+x\right)}=0\)
3) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}=2x+\dfrac{1}{2x}-7\)
4) \(\sqrt{x}-\dfrac{4}{\sqrt{x+2}}+\sqrt{x+2}=0\)
5)\(\left(x-7\right)\sqrt{\dfrac{x+3}{x-7}}=x+4\)
6) \(2\sqrt{x-4}+\sqrt{x-1}=\sqrt{2x-3}+\sqrt{4x-16}\)
7) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\dfrac{x+3}{2}\)
Giúp mình với ajk, mink đang cần gấp
Giải phương trình sau
\(x^2-2\sqrt{5}x+5=0
\)
\(4x^4-5x^2-9=0\)
a: \(\Leftrightarrow\left(x-\sqrt{5}\right)^2=0\)
\(\Leftrightarrow x-\sqrt{5}=0\)
hay \(x=\sqrt{5}\)
b: \(\Leftrightarrow4x^4-9x^2+4x^2-9=0\)
\(\Leftrightarrow4x^2-9=0\)
=>x=3/2hoặc x=-3/2
Đúng 0
Bình luận (0)
\(^{x^2-5x+4-\sqrt{5-x}-\sqrt{x-2}=0}\)\(\sqrt{x+2}+\sqrt{3-x}=x^3+x^2-4x-1\)Giải phương trình
2)
1, \(x^2-5x+4-\sqrt{5-x}-\sqrt{x-2}=0\)ĐKXĐ \(2\le x\le5\)
ĐK dấu bằng xảy ra \(x^2-5x+4\ge0\)
Kết hơp với ĐKXĐ=> \(4\le x\le5\)
Khi đó Phương trình tương đương
\(x^2-7x+11+\left(x-4-\sqrt{5-x}\right)+\left(x-3-\sqrt{x-2}\right)=0\)
<=> \(x^2-7x+11+\frac{x^2-7x+11}{x-4+\sqrt{5-x}}+\frac{x^2-7x+11}{x-3+\sqrt{x-2}}=0\)
=> \(\orbr{\begin{cases}x^2-7x+11=0\\1+\frac{1}{x-4+\sqrt{5-x}}+\frac{1}{x-3+\sqrt{x-2}}=0\left(2\right)\end{cases}}\)
Phương trình (2) vô nghiệm với \(4\le x\le5\)=> VT>0
\(x^2-7x+11=0\)
Với \(4\le x\le5\)
\(S=\left\{\frac{7+\sqrt{5}}{2}\right\}\)
Đúng 0
Bình luận (0)
2.\(\sqrt{x+2}+\sqrt{3-x}=x^3+x^2-4x-1\)ĐKXĐ \(-2\le x\le3\)
<=> \(3x^3+3x^2-12x-3=3\sqrt{x+2}+3\sqrt{3-x}\)
<=> \(3x^3+3x^2-12x-12+\left(x+4-3\sqrt{x+2}\right)+\left(5-x-3\sqrt{3-x}\right)=0\)
<=> \(3\left(x^2-x-2\right)\left(x+2\right)+\frac{x^2-x-2}{x+4+3\sqrt{x+2}}+\frac{x^2-x-2}{5-x+3\sqrt{3-x}}=0\)
=> \(\orbr{\begin{cases}x^2-x-2=0\\3\left(x+2\right)+\frac{1}{x+4+3\sqrt{x+2}}+\frac{1}{5-x+3\sqrt{x-3}}=0\left(2\right)\end{cases}}\)
Phương trình (2) vô nghiệm với\(-2\le x\le3\)=> VT>0
\(S=\left\{2;-1\right\}\)
Đúng 0
Bình luận (0)
Giải phương trình: \(\sqrt{x-2}+\sqrt{4-x}+\sqrt{2x-5}=2x^2-5x\).
Giải Phương Trình
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{5x-6}-3=0\)
Giải phương trình :
a.\(x^2+5x^2-3=0\)
b.\(x^2-\left(2\sqrt{3}-1\right)x+4\sqrt{3}-6=0\)
c.\(x^2-6x+9=0\)
d.\(x^2-4\sqrt{3}x-4=0\)
c: \(\Leftrightarrow x-3=0\)
hay x=3
Đúng 1
Bình luận (0)
Giải các bất phương trình sau:
a.(x+1)(-x2+3x-2)<0
b.\(\sqrt{x^2-5x+4}+2\sqrt{x+5}>2\sqrt{x-4}+\sqrt{x^2+4x-5}\)