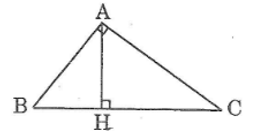
cho tam giác ABC cân tại B có chu vi=50cm.Kẻ đường cao BH.Biết chu vi tam giác ABH=40cm.Tính độ dài BH

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A,vẽ đường cao AH.Chu vi của tam giác ABH là 30cm và chu vi tam giác ACH là 40cm.Tính chu vi của tam giác ABC
CHO TAM GIÁC ABC VUÔNG TẠI A. VẼ ĐG CAO AH
A) NẾU CHO BH=18, CH=32. TÍNH ĐỘ DÀI CÁC CẠNH CỦA TAM GIÁC ABC
B) (ĐỘC LẬP VỚI CÂU A) NẾU CHO CHU VI TAM GIÁC ABH=15m, CHU VI TAM GIÁC ACH BẰNG 20m.TÍNH CHU VI TAM GIÁC ABC
Co △ABC vuông tại A, có đường cao AH:
a) Cho AH=6cm, BH=4cm. Tính HC,BC,AB,AC, S△HAC.
b)Cho chu vi △ABH= 30cm, chu vi △ACH=40cm.Tính chu vi △ABC
Cho tam giác ABC, góc A=90 độ, đường cao AH. Chu vi tam giác ABH=18cm, chu vi tam giác ACH=24cm. Tính chu vi tam giác ABC và độ dài AH
Ai biết là giúp mình với. Mình cảm ơn!
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, AC 4cm. Tính độ dài đường cao AH, tính
c
o
s
A
C
B
^
và chu vi tam giác ABH. A. AH 2,8 cm;
c
o
s
A
C
B
^
3
5
B. AH 2,4 cm; ...
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH, tính c o s A C B ^ và chu vi tam giác ABH.
A. AH = 2,8 cm; c o s A C B ^ = 3 5
B. AH = 2,4 cm; c o s A C B ^ = 4 5
C. AH = 2,5 cm; c o s A C B ^ = 3 4
D. AH = 1,8 cm; c o s A C B ^ = 2 3
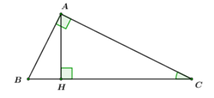
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B
Đúng 2
Bình luận (0)
Bài 1:Cho hcn ABCD .Đường phân giác của góc B cắt đường chéo AC thành 2 đoạn 4\(\frac{2}{7}\)m và 5\(\frac{5}{7}\).Tính các kích thước của hcn
Bài 2: Cho tám giác ABC vuông tại A,vẽ đường cao AH.Chu vi của tam giác ABH là 30cm và chu vi tam giác ACH là 40cm.Tính chu vi của tam giác ABC
Bài 1:
Theo đề, ta có: \(\dfrac{AB}{BC}=\dfrac{30}{7}:\dfrac{40}{7}=\dfrac{3}{4}\) và \(AC=4+5+\dfrac{2}{7}+\dfrac{5}{7}=10\)
=>AB/3=BC/4
Đặt AB/3=BC/4=k
=>AB=3k; BC=4k
Xét ΔABC vuông tại B có \(AC^2=AB^2+BC^2\)
\(\Leftrightarrow25k^2=100\)
=>k=2
=>AB=CD=6(cm); BC=AD=8(cm)
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a đường cao ah. chu vi tam giác ABH = 30 cm, chu vi của tam giác ACH = 40 cm. tính chu vi tam giác ABC
Tam giác ABH và CAH vuông và có ^BAH=^C (cùng phụ với góc B)
Nên Tam giác ABH và CAH đồng dạng (g-g) =>AB/AC = k (tỷ số đồng dạng)
Mà C(ABH) / C(CAH) = k (tỷ số chu vi bằng tỷ số đồng dạng)
suy ra 30/40 = k hay k = 3/4.
do đó AB/AC = 3/4 hay AB/3 = AC/4 = t
=> AB = 3t; AC = 4t Theo Pitago ta tính được BC = 5t.
Vậy chu vi tam giác ABC là AB+AC+BC = 3t+4t+5t = 12t.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết chu vi tam giác ABH bằng 30cm và chu vi ACH bằng 40cm. Tính chu vi tam giác ABC.
\(\Delta ABH\sim\Delta CAH\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{C_{ABC}}{C_{CAH}}=\dfrac{30}{40}=\dfrac{3}{4}\)
=> \(\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}\)
\(\Rightarrow\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\\\)
=> \(\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(\Delta ABH\sim\Delta CBA\)
\(\Rightarrow\dfrac{C_{ABH}}{C_{ABC}}=\dfrac{AB}{BC}\)
=> Chu vi tam giác ABC là 30 . 5 : 3 = 50
Đúng 2
Bình luận (0)
Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có:
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH kẻ HE vuông góc với AB , HF vuông góc với AC
a)Tính EF biết BH=13.5cm CH=6cm
b)CMR: AE.AB=AF.AC
c)Qua A kẻ AK vuông góc với EF , AK cắt BC tại I
d)CMR:Nếu diện tích tam gúac ABC=2 lần diện tích tam giác AEHF thì tam giác ABC vuông cân
e)Biết chu vi tam giác ABH = 30cm chu vi tam giác ACH=40cm tình chu vi tam gúac ABC