Đáp án là C

Tam giác ABC có:

A B 2 + A C 2 = 12 2 + 16 2 = 400 = B C 2

⇒ ΔABC vuông tại A

⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của BC

⇒ Bán kính = 10 cm

Đáp án là B

Xét tam giác ABC có:

A B 2 + A C 2 = 7 2 + 24 2 = 625 = B C 2

⇒ ΔABC vuông tại A

⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC

⇒ Bán kính đường tròn ngoại tiếp là 12,5 cm

\(R=\dfrac{a+b}{2}\)

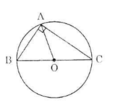
Hình a) + b)

a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.

Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.

=> O là tâm của đường tròn đi qua A, B, C.

Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)

b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:

        OA = OB = OC

Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)

a, Giả sử ∆ABC vuông tại A. Gọi O là trung điểm của BC

=> OA = OB = OC => O là tâm đường tròn đi qua A,B,C

b, Ta có OA = OB = OC => OA = 1 2 BC => ∆ABC vuông tại A

hình bạn tự vẽ nha

gọi o là trung điểm của BC suy ra O là tâm đường tròn ngoại tiếp tam giác ABC suy ra OA=OB=OC=15 cm suy ra BC=30cm

xét tam giác AhO có góc AHO bằng 90',

OH=\(\sqrt{\left(OA^2-AH^2\right)}\)  = 4,2

ta có : OB=OH+BH suy ra BH=OB-OH suy ra BH=10,8\(\)

XÉT tam giác ABC co góc BAC=90' , đường cao AH

\(AB^2=BH.BC\) = 10,8.30=324  suy ra AB=18

\(AC^2=BC^2-AB^2\) suy ra AC=\(\sqrt{\left(BC^2-AB^2\right)}\)  suy ra AB=24

suy ra AB+AC=42

a) Xét tam giác ABC vuông tại A.

Gọi O là trung điểm của cạnh huyền BC, ta có:

OA=OB=OC.

Vậy O chính là tâm cuả đường tròn ngoại tiếp tam giác ABC

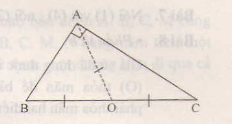
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC.

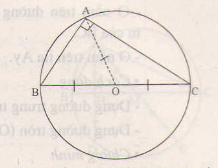
Ta có OA=OB=OC(=R)

2BC, do đó tam giác ABC vuông tại A

Nhận xét: Định lý trong bài tập này thường được dùng để giải nhiều bài tập về nhận biết tam giác vuông.

14 cháu 

Làm trên này là fai có cáh giải nuk cháu ak, ghi kq chỉ tổ tốn côg

Hỏi như nào trả lời như ấy...ko dủ làm đầy đủ thì không làm