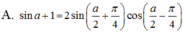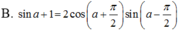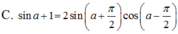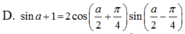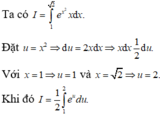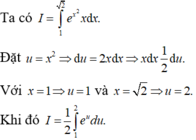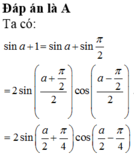biến tích thành tổng
cosa.cosb.cosc

Những câu hỏi liên quan
Biến đổi tích thành tổng
c) \(4sin3x\cdot sin2x\cdot cosx=2(cosx-cos5x)\cdot cosx\)
\(=2cos^2x-2cos5x\cdot cosx\)
\(=2cos^2x-cos4x-cos6x\)
\(=1+cos2x-cos4x-cos6x\)
d) \(4sin\dfrac{13x}{2}\cdot cosx\cdot cos\dfrac{x}{2}=4sin\dfrac{x}{2}\cdot cos\dfrac{x}{2}\cdot cosx\)
\(=2sinx\cdot cosx\)
\(=sin2x\)
Đúng 0
Bình luận (0)
Biến đổi tích thành tổng
4sin3a.sin2a.sina
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
`a^2 + ab + 2a + 2b = a(a+2) + b(a+2) = (a+b)(a+2)`
Đúng 1
Bình luận (0)
Sử dụng công thức biến đổi tích thành tổng và đặt \(a + b = u;\,\,a - b = v\) biến đổi các biểu thức sau thành tích: \(\cos u + \cos v;\,\,\cos u - \cos v;\,\,\sin u + \sin v;\,\,\sin u - \sin v\)
\(\begin{array}{l}1.\,\,\,\,\cos a.\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right] \Leftrightarrow 2\cos a.\cos b = \cos \left( {a + b} \right) + \cos \left( {a - b} \right)\\ \Leftrightarrow 2\cos \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \cos u + \cos v\\2.\,\,\,\,\sin a.\sin b = - \frac{1}{2}.\left[ {\cos \left( {a + b} \right) - \cos \left( {a - b} \right)} \right] \Leftrightarrow - 2.\sin a.\sin b = \cos \left( {a + b} \right) - \cos \left( {a - b} \right)\\ \Leftrightarrow - 2.\sin \frac{{u + v}}{2}.\sin \frac{{u - v}}{2} = \cos u - \cos v\\3.\,\,\,\,\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right] \Leftrightarrow 2\sin a.\cos b = \sin \left( {a + b} \right) + \sin \left( {a - b} \right)\\ \Leftrightarrow 2\sin \frac{{u + v}}{2}.\cos \frac{{u - v}}{2} = \sin u + \sin v\\4.\,\,\,\,\sin \left( {a + b} \right) - \sin \left( {a - b} \right) = \sin a.\cos b + \cos a.\sin b - \sin a.\cos b + \cos a.\sin b = 2\cos a.\sin b\\ \Leftrightarrow \sin u - \sin v = 2.\cos \frac{{u + v}}{2}.\sin \frac{{u - v}}{2}\end{array}\)
Đúng 0
Bình luận (0)
Xét tích phân
I
∫
1
2
x
.
e
x
2
. Sử dụng phương pháp đổi biến số với
u
x
2
, tích phân I được biến đổi thành dạng nào sau đây: A.
I
2
∫
1
2...
Đọc tiếp
Xét tích phân I = ∫ 1 2 x . e x 2 . Sử dụng phương pháp đổi biến số với u = x 2 , tích phân I được biến đổi thành dạng nào sau đây:
A. I = 2 ∫ 1 2 e u d u
B. I = 1 2 ∫ 1 2 e u d u
C. I = 1 2 ∫ 1 2 e u d u
D. 2 ∫ 1 2 e u d u
Xét tích phân
I
∫
1
2
x
e
x
2
d
x
. Sử dụng phương pháp đổi biến số với
u
x
2
, tích phân I được biến đổi thành dạng nào sau đây:
Đọc tiếp
Xét tích phân I = ∫ 1 2 x e x 2 d x . Sử dụng phương pháp đổi biến số với u = x 2 , tích phân I được biến đổi thành dạng nào sau đây:
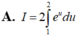
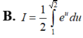

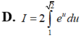
Biến đổi thành tích - cos 5 a . cos 4 a - cos 4 a . cos 3 a + 2 cos 2 2 a . cos a
Biến đổi biểu thức sina + 1 thành tích.
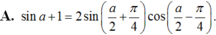
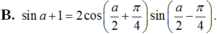
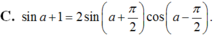
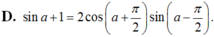
Chọn A.
Áp dụng công thức nhân đôi và chú ý: ![]() (đây là 2 góc phụ nhau)
(đây là 2 góc phụ nhau)
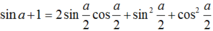
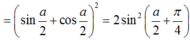
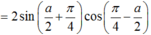
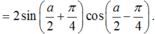
Đúng 0
Bình luận (0)
Biến đổi biểu thức sin a + 1 thành tích.