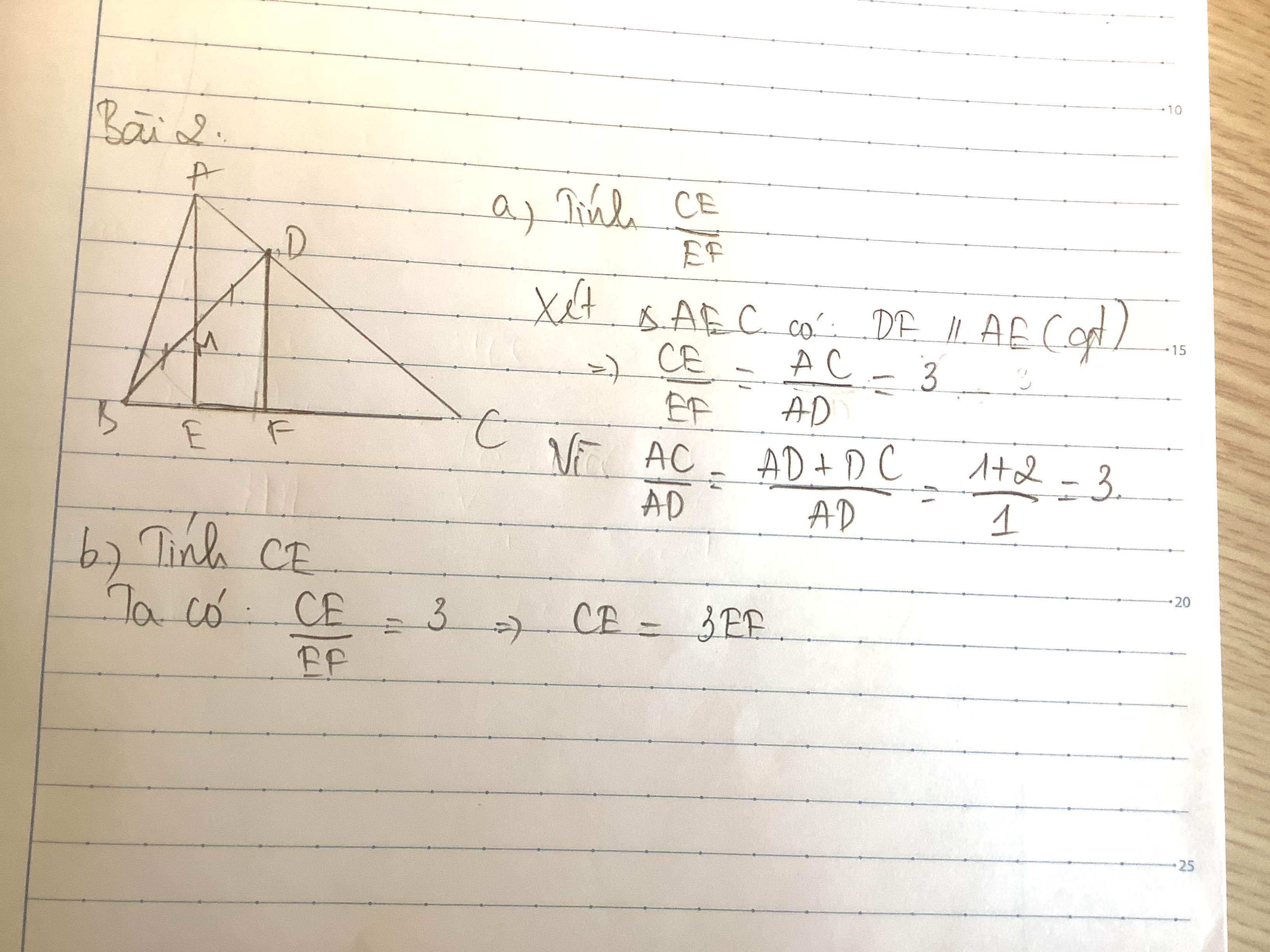cho Δabc có BC=5,AC=4,AB=6 và AD là đường phan giác . tinh BD

Những câu hỏi liên quan
Cho tam giác ABC có AD là phân giác (D thuộc BC). Biết AB=4, AC=8, BC=6.Tinh BD và DC
Vì AD là phân giác nên
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{DC}{AC}=\dfrac{BD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{AC}=\dfrac{BD}{AB}=\dfrac{6}{12}=\dfrac{1}{2}\Rightarrow DC=4cm;DB=2cm\)
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A, đường cao AH, cho AD là tia phân giác của ∠BAC, cho BD = 4 và CD = 5. Tính AB, AC, BH, CH, AH.
Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{4}{5}\)
\(\Leftrightarrow AB=\dfrac{4}{5}AC\)
Ta có: BC=BD+CD
nên BC=4+5
hay BC=9cm
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{41}{25}=9\)
\(\Leftrightarrow AC^2=\dfrac{225}{41}\)
\(\Leftrightarrow AC=\dfrac{15\sqrt{41}}{41}\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{12\sqrt{41}}{41}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{16}{41}\left(cm\right)\\CH=\dfrac{353}{41}\left(cm\right)\\AH=\dfrac{4\sqrt{353}}{41}\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho ΔABC ( AB<AC), đường phân giác AD. Qua trung điểm M của BC, kẻ đường thẳng // AD, cắt AC,AB lần lượt tại E,K. Gọi O là giao điểm AM và DK
a, CM AO.OK=DO.OM
b, cho AB=5cm, AC=10cm, BC=12cm. tinhd BD
c, cm AE=AK, AB/CE=BD/CM
a: Xét ΔOAD và ΔOMK có
\(\widehat{OAD}=\widehat{OMK}\)(hai góc so le trong, AD//MK)
\(\widehat{AOD}=\widehat{MOK}\)
Do đó: ΔOAD đồng dạng với ΔOMK
=>\(\dfrac{OA}{OM}=\dfrac{OD}{OK}\)
=>\(OA\cdot OK=OM\cdot OD\)
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{CA}\)
=>\(\dfrac{BD}{5}=\dfrac{CD}{10}\)
=>\(\dfrac{BD}{1}=\dfrac{CD}{2}\)
mà BD+CD=BC=12
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{1}=\dfrac{CD}{2}=\dfrac{BD+CD}{1+2}=\dfrac{12}{3}=4\)
=>\(BD=4\left(cm\right);CD=8\left(cm\right)\)
c: ME//AD
=>\(\widehat{AEK}=\widehat{DAC}\)(hai góc so le trong)(1)
KM//AD
=>\(\widehat{AKE}=\widehat{BAD}\)(hai góc đồng vị)(2)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{AEK}=\widehat{AKE}\)
=>AE=AK
Xét ΔCAD có EM//AD
nên \(\dfrac{CE}{CA}=\dfrac{CM}{CD}\)
=>\(\dfrac{CE}{CM}=\dfrac{CA}{CD}\)
mà \(\dfrac{CA}{CD}=\dfrac{BA}{BD}\)
nên \(\dfrac{CE}{CM}=\dfrac{BA}{BD}\)
=>\(\dfrac{AB}{BD}=\dfrac{EC}{CM}\)
=>\(\dfrac{AB}{EC}=\dfrac{BD}{CM}\)(ĐPCM)
Đúng 1
Bình luận (0)
B1. Cho ΔABC có Aˆ90∘. AB AC, điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD AE. Đường thẳng qua D và vuông góc với BE cắt đường thẳng CA ở K. CMR: AK ACB2. Cho ΔABC, I là trung điểm của AB, đường thẳng qua I và song song với BC cắt AC ở K. Đường thẳng qua K và song song với AB cắt BC ở H. CMRa) KH IBb) AK KCB3. Cho ΔABC có Aˆ 60∘. Tia phân giác của Bˆ cắt AC ở D, tia phân giác của Cˆ cắt AB ở E. Gọi O là giao điểm của BD và CE.a) Tính BOCˆb) C/m CD OEB4. Cho ΔABC. Ở phía ngoài ΔAB...
Đọc tiếp
B1. Cho ΔABC có Aˆ=90∘. AB = AC, điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Đường thẳng qua D và vuông góc với BE cắt đường thẳng CA ở K. CMR: AK = AC
B2. Cho ΔABC, I là trung điểm của AB, đường thẳng qua I và song song với BC cắt AC ở K. Đường thẳng qua K và song song với AB cắt BC ở H. CMR
a) KH = IB
b) AK = KC
B3. Cho ΔABC có Aˆ = 60∘. Tia phân giác của Bˆ cắt AC ở D, tia phân giác của Cˆ cắt AB ở E. Gọi O là giao điểm của BD và CE.
a) Tính BOCˆ
b) C/m CD = OE
B4. Cho ΔABC. Ở phía ngoài ΔABC vẽ các tam giác vuông tại A là ABD và ACE có AB = AD, AC = AE. Kẻ AH vuông góc với BC, gọi I là giao điểm của HA và DE. CMR: DI = IE
Giúp em với !! T7 phải nộp rồiii
Cho ΔABC , góc A =90 độ , góc B=60độ .
a, So sánh AD và BD
b, Trên BC lấy D sao cho BD=AB . Qua D dựng đường vuông góc với BC cắt tia đối của AB tại E . Chứng minh : ΔABC=ΔDBE
c, H là giao điểm của AC và ED . Chứng minh : BH là phân giác của góc ABC
d, Qua B vẽ đường thẳng vuông góc AB cắt ED tại K . Chứng minh : ΔHBK đều
b) Xét ΔABC vuông tại A và ΔDBE vuông tại D có
AB=BD(gt)
\(\widehat{ABC}\) chung
Do đó: ΔABC=ΔDBE(cạnh góc vuông-góc nhọn kề)
c) Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD(gt)
Do đó: ΔBAH=ΔBDH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
hay BH là tia phân giác của \(\widehat{ABC}\)
d) Ta có: BH là tia phân giác của \(\widehat{ABC}\)(cmt)
nên \(\widehat{ABH}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ABH}+\widehat{HBK}=90^0\)
\(\Leftrightarrow\widehat{HBK}+30^0=90^0\)
hay \(\widehat{HBK}=60^0\)
Xét ΔCHD vuông tại D và ΔCBA vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHD\(\sim\)ΔCBA(g-g)
Suy ra: \(\widehat{CHD}=\widehat{CBA}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{CHD}=60^0\)
mà \(\widehat{CHD}=\widehat{HKB}\)(hai góc so le trong, BK//AC)
nên \(\widehat{HKB}=60^0\)
Xét ΔHBK có
\(\widehat{HKB}=60^0\)(cmt)
\(\widehat{HBK}=60^0\)(cmt)
Do đó: ΔHBK đều(Dấu hiệu nhận biết tam giác đều)
Đúng 0
Bình luận (1)
b1: cho Δabc lay MϵBC, ME//AC, MD//AB(DϵAC). Tinh AE/AB + AD/AC = ?
b2: cho Δabc, lay DϵAC sao cho AD/CD=1/2. Goi M la trung diem cua BD. Tia AM cat BC tai E. DF//AE(FϵBC). a, tinh CE/EF
b, tinh CE
Hua danh gia 5* lun
Bài 1:
Xét ΔABC có
MD//AB
nên \(\dfrac{AD}{AC}=\dfrac{BM}{BC}\)
Xét ΔABC có
ME//AC
nên \(\dfrac{AE}{AB}=\dfrac{CM}{CB}\)
Ta có: \(\dfrac{AE}{AB}+\dfrac{AD}{AC}\)
\(=\dfrac{BM}{BC}+\dfrac{CM}{BC}\)
=1
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A có AB = 3cm; BC = 5cm. Gọi CD là đường phân giác của ΔABC. Tính AC; BD và CD. (khỏi vẽ hình ạ)
Xét tam giác vuông ABC có:
\(AB^2+AC^2=BC^2\\ =>3^2+AC^2=5^2\\ =>AC^2=16\\ =>AC=4cm\)
Đúng 4
Bình luận (1)
Bài 5: Cho ΔABC cân tại A có AB AC 6cm; BC 4cm. Các đường phân giác BD và CE cắt nhau tại I (E trên AB và D trên AC)a. Tính độ dài AD, ED.b. Cm ΔADB đồng dạng với ΔAECc. Cm IE.CD ID.BEd. Cho SABC 60 cm². Tính SAED.
Đọc tiếp
Bài 5: Cho ΔABC cân tại A có AB = AC = 6cm; BC = 4cm. Các đường phân giác BD và CE cắt nhau tại I (E trên AB và D trên AC)
a. Tính độ dài AD, ED.
b. Cm ΔADB đồng dạng với ΔAEC
c. Cm IE.CD = ID.BE
d. Cho SABC = 60 cm². Tính SAED.
a: Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/2=6/5=1,2
=>AD=3,6cm; CD=2,4cm
Xét ΔABCcó ED//BC
nên ED/BC=AD/AC
=>ED/4=3,6/6=3/5
=>ED=2,4cm
b: Xét ΔADB và ΔAEC có
góc A chung
góc ABD=góc ACE
=>ΔABD đồng dạng với ΔACE
c: Xét ΔIEB và ΔIDC có
góc IEB=góc IDC
góc EIB=góc DIC
=>ΔIEB đồng dạng với ΔIDC
=>EB/DC=IE/ID
=>IE*DC=EB*ID
Đúng 0
Bình luận (0)
Bài 2. ΔABC có 𝐴̂ 900 . Lấy M trên BC vẽ MH ⊥ AB, MK ⊥ AC.a) So sánh 𝐵𝑀𝐻 ̂ và 𝐵𝐶𝐴 ̂, 𝐻𝐵̂𝑀 và 𝐾𝑀𝐶 ̂b) Tính 𝐻𝑀𝐾 ̂Bài 3. ΔABC có 𝐴̂ 60 0 , AD là phân giác của góc A (D ∈ BC). Từ D vẽ đường thẳng song song với AB cắt AC ở M. Từ M vẽ MK // AD và cắt BC tại K.a) Tính 𝐵𝐴𝐷 ̂, 𝐷𝑀𝐾 ̂, 𝐴𝐷𝑀̂;b) Chứng minh rằng MK là phân giác của góc 𝐷𝑀𝐶 ̂.Bài 4. Cho ΔABC. Tia phân giác của góc B và C cắt nhau ở I. Từ I kẻ đường thẳng song song vớ BC cắt AB ở F và AC ở E.a) Chứng minh 𝐷𝐼𝐵̂ 𝐷𝐵𝐼 ̂b) Chứng minh 𝐸𝐼𝐶̂ 𝐸𝐶𝐼 ̂...
Đọc tiếp
Bài 2. ΔABC có 𝐴̂ = 900 . Lấy M trên BC vẽ MH ⊥ AB, MK ⊥ AC.
a) So sánh 𝐵𝑀𝐻 ̂ và 𝐵𝐶𝐴 ̂, 𝐻𝐵̂𝑀 và 𝐾𝑀𝐶 ̂
b) Tính 𝐻𝑀𝐾 ̂
Bài 3. ΔABC có 𝐴̂ = 60 0 , AD là phân giác của góc A (D ∈ BC). Từ D vẽ đường thẳng song song với AB cắt AC ở M. Từ M vẽ MK // AD và cắt BC tại K.
a) Tính 𝐵𝐴𝐷 ̂, 𝐷𝑀𝐾 ̂, 𝐴𝐷𝑀̂;
b) Chứng minh rằng MK là phân giác của góc 𝐷𝑀𝐶 ̂.
Bài 4. Cho ΔABC. Tia phân giác của góc B và C cắt nhau ở I. Từ I kẻ đường thẳng song song vớ BC cắt AB ở F và AC ở E.
a) Chứng minh 𝐷𝐼𝐵̂ = 𝐷𝐵𝐼 ̂
b) Chứng minh 𝐸𝐼𝐶̂ = 𝐸𝐶𝐼 ̂ . Bài 5. Cho ΔABC có 𝐴̂ = 120 0 . Từ C kẻ đường thẳng song song với phân giác AD của tam giác ABC và đường thẳng này cắt đường thẳng BA tại M. Tính 𝐴𝑀𝐶 ̂ và 𝐴𝐶𝑀̂.
Bài 5. Cho ΔABC có 𝐴̂ = 120 0 . Từ C kẻ đường thẳng song song với phân giác AD của tam giác ABC và đường thẳng này cắt đường thẳng BA tại M. Tính 𝐴𝑀𝐶 ̂ và 𝐴𝐶𝑀̂.
MÌNH BT LÀ DÀI NHƯNG MN AI ÓC THỜI GIAN THÌ GIÚP MÌNH Ạ
CHÂN THÀNH CẢM ƠN