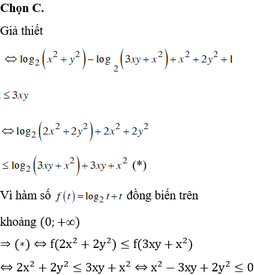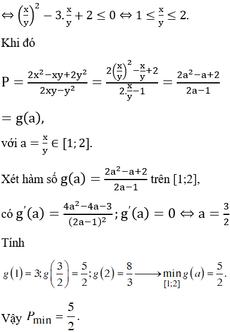Tìm các số nguyên x, y thỏa mãn : 2y2x + x + y + 1 = x2 + 2y2 + xy

Những câu hỏi liên quan
Tìm tất cả các bội số nguyên (x;y) thỏa mãn phương trình:
a) x2 - 2x + 2y2 = 2(xy +1)
b) x2 + 2y2 + 2xy - 2x = 7
a.
\(\Leftrightarrow2x^2-4x+4y^2=4xy+4\)
\(\Leftrightarrow\left(x^2-4xy+4y^2\right)+\left(x^2-4x+4\right)=8\)
\(\Leftrightarrow\left(x-2y\right)^2+\left(x-2\right)^2=8\) (1)
Do \(\left(x-2y\right)^2\ge0;\forall x;y\)
\(\Rightarrow\left(x-2\right)^2\le8\)
\(\Rightarrow\left(x-2\right)^2=\left\{0;1;4\right\}\)
TH1: \(\left(x-2\right)^2\Rightarrow x=2\) thế vào (1)
\(\Rightarrow\left(2-2y\right)^2=8\Rightarrow\left(1-y\right)^2=2\) (ko tồn tại y nguyên t/m do 2 ko phải SCP)
TH2: \(\left(x-2\right)^2=1\Rightarrow\left(x-2y\right)^2=8-1=7\), mà 7 ko phải SCP nên pt ko có nghiệm nguyên
TH3: \(\left(x-2\right)^2=4\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\) thế vào (1):
- Với \(x=0\Rightarrow\left(-2y\right)^2+4=8\Rightarrow y^2=1\Rightarrow y=\pm1\)
- Với \(x=2\Rightarrow\left(2-2y\right)^2+4=8\Rightarrow\left(1-y\right)^2=1\Rightarrow\left[{}\begin{matrix}y=0\\y=2\end{matrix}\right.\)
Vậy pt có các cặp nghiệm là:
\(\left(x;y\right)=\left(0;1\right);\left(0;-1\right);\left(2;0\right);\left(2;2\right)\)
Đúng 2
Bình luận (0)
b.
\(\Leftrightarrow2x^2+4y^2+4xy-4x=14\)
\(\Leftrightarrow\left(x^2+4xy+4y^2\right)+\left(x^2-4x+4\right)=18\)
\(\Leftrightarrow\left(x+2y\right)^2+\left(x-2\right)^2=18\) (1)
Lý luận tương tự câu a ta được
\(\left(x-2\right)^2\le18\Rightarrow\left(x-2\right)^2=\left\{0;1;4;9;16\right\}\)
Với \(\left(x-2\right)^2=\left\{0;1;4;16\right\}\) thì \(18-\left(x-2\right)^2\) ko phải SCP nên ko có giá trị nguyên x;y thỏa mãn
Với \(\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\) thế vào (1)
- Với \(x=5\Rightarrow\left(5+2y\right)^2+9=18\Rightarrow\left(5+2y\right)^2=9\)
\(\Rightarrow\left[{}\begin{matrix}5+2y=3\\5+2y=-3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=-1\\y=-4\end{matrix}\right.\)
- Với \(x=-1\Rightarrow\left(-1+2y\right)^2=9\Rightarrow\left[{}\begin{matrix}-1+2y=3\\-1+2y=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=2\\y=-1\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(5;-1\right);\left(5;-4\right);\left(-1;3\right);\left(-1;-3\right)\)
Đúng 2
Bình luận (0)
tìm các nguyên tố x,y thỏa mãn x2-2y2=1
Tìm các cặp số nguyên x,y, thỏa : x2 -2y2 xy 2x 4y -5=0
Cho các số thực x, y dương và thỏa mãn
log
2
x
2
+
y
2
3
xy
+
x
2
+
2
log
2
x
2
+...
Đọc tiếp
Cho các số thực x, y dương và thỏa mãn log 2 x 2 + y 2 3 xy + x 2 + 2 log 2 x 2 + 2 y 2 + 1 ≤ log 2 8 xy .Tìm giá trị nhỏ nhất của biểu thức P = 2 x 2 - xy + 2 y 2 2 xy - y 2 .
cho các số dương x,y,z thỏa mãn x+y+z=1 tìm min của biểu thức
P=√(2x2+xy+2y2) +√(2y2+yz+2z2)+ √(2z2+xz+2x2)
Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737
Đúng 1
Bình luận (0)
Tìm tất cả các số nguyên x, y thỏa mãn x2+y2+xy-x-y=1
tìm các số nguyen tố x,y thỏa mãn đề bài x2-2y2-1=0
\(\Leftrightarrow x^2-1=2y^2\)
Do vế phải chẵn \(\Rightarrow\) vế trái chẵn \(\Leftrightarrow x\) lẻ
\(\Rightarrow x=2k+1\)
Pt trở thành: \(\left(2k+1\right)^2-1=2y^2\Leftrightarrow2\left(k^2+k\right)=y^2\)
Vế trái chẵn \(\Rightarrow\) vế phải chẵn \(\Rightarrow y^2\) chẵn \(\Rightarrow y\) chẵn
\(\Rightarrow y=2\)
\(\Rightarrow x^2-9=0\Rightarrow x=3\)
Vậy \(\left(x;y\right)=\left(3;2\right)\)
Đúng 3
Bình luận (0)
tìm các cặp số nguyên x, y thỏa mãn: y2(x2-x+1)+xy = 3x-1
bài 1: cho các số dương x, y, z thỏa mãn x+y+z=1. Tìm min
a) A = x2+y2+z2
b) B = x2+y2+3z2
c) C=x2+2y2+3z2
d) D=x2+by2+cz2
tìm các số nguyên x,y thỏa mãn :
x2+3x+5=xy+2y
\(x^2+3x+5=xy+2y\\ \Leftrightarrow x^2+3x-xy-2y+5=0\\ \Leftrightarrow x\left(x+2\right)-y\left(x+2\right)+\left(x+2\right)+3=0\\ \Leftrightarrow\left(x+2\right)\left(x-y+1\right)=-3=\left(-1\right)\cdot3=\left(-3\right)\cdot1\)
\(TH_1:\left\{{}\begin{matrix}x+2=-3\\x-y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=-5\end{matrix}\right.\to\left(-5;-5\right)\\ TH_2:\left\{{}\begin{matrix}x+2=3\\x-y+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\to\left(1;3\right)\\ TH_3:\left\{{}\begin{matrix}x+2=1\\x-y+1=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=3\end{matrix}\right.\to\left(-1;3\right)\\ TH_4:\left\{{}\begin{matrix}x+2=-1\\x-y+1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-5\end{matrix}\right.\to\left(-3;-5\right)\)
Vậy \(\left(x;y\right)=\left(-5;-5\right);\left(1;3\right);\left(-1;3\right);\left(-3;-5\right)\)
Đúng 3
Bình luận (0)