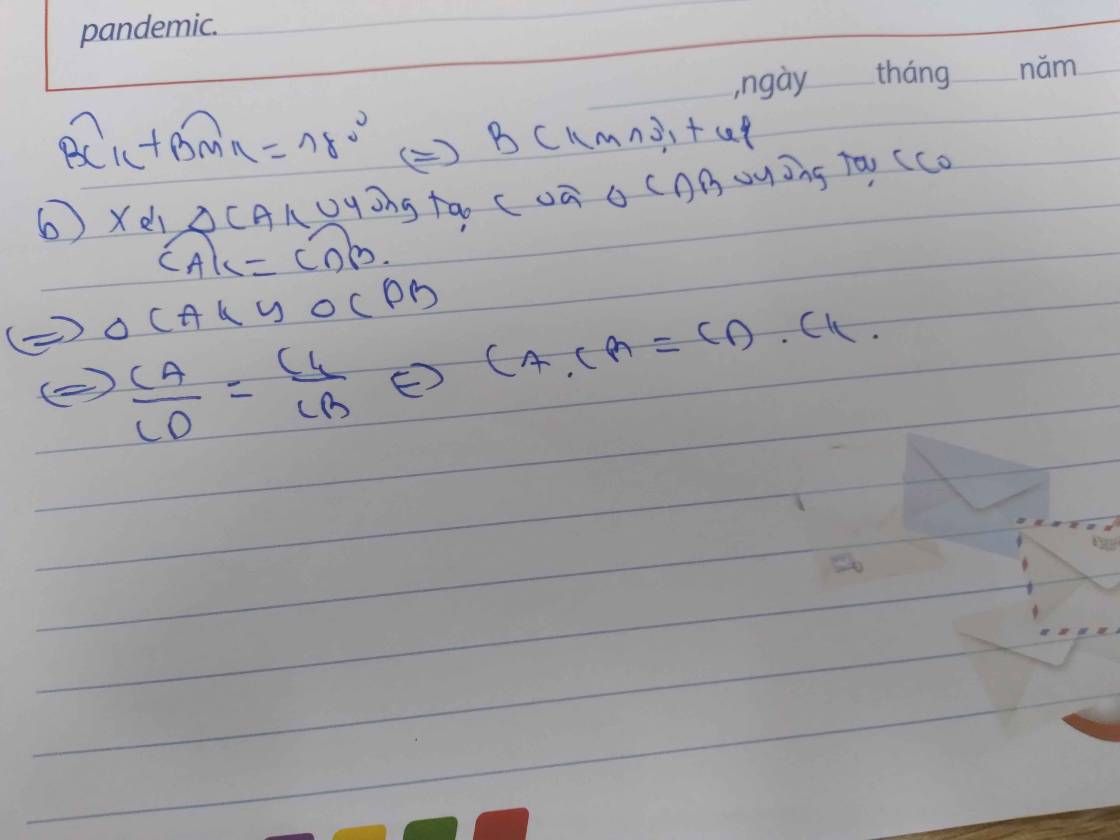Cho điểm C nằm trên nửa đường tròn (O ; R) đường kính AB sao cho cung AC > cung BC (C khác B). Đường thẳng vuông góc với AB tại O cắt dây AC tại D. Tiếp tuyến của (O) cắt đường thẳng đi qua D và song song với AB tại E. Tứ giác OEDA là hình gì ?

Những câu hỏi liên quan
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh: 1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn. 2) CK.CD CA.CB 3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
Đọc tiếp
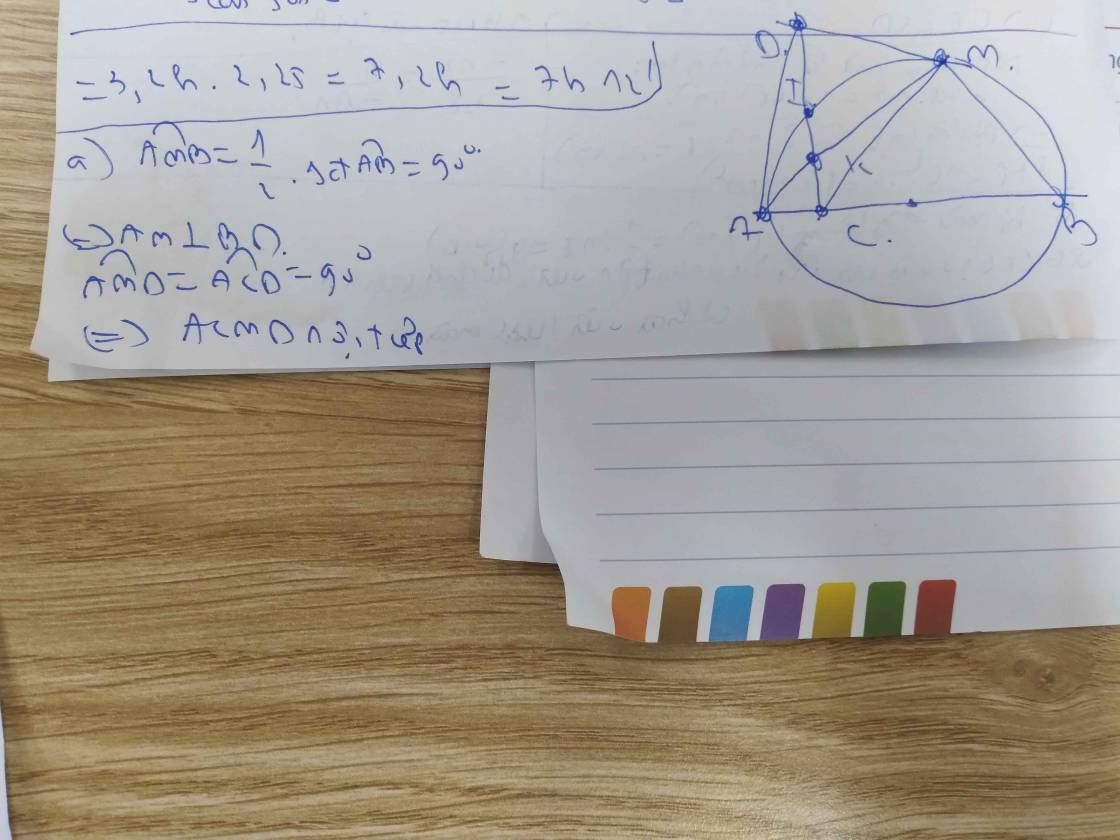
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:
1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn.
2) CK.CD = CA.CB
3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :a) Các tứ giác : ACMD ; BCKM nội tiếp đường trònb) CK.CD CA.CBc) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :
a) Các tứ giác : ACMD ; BCKM nội tiếp đường tròn
b) CK.CD = CA.CB
c) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CDCA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CD=CA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Cho đường tròn tâm O điểm A nằm ngoài đường tròn. Vẽhai tiếp tuyến AM, AN với đường tròn tâm O ( M,N là hai tiếp điểm). Qua A vẽ 1 đường thẳng d cắt đường tròn tâm O tại B và C sao cho 2 điểm nằm giữa A và C, hai điểm O và N nằm trên hai nửa mặt phẳng đối nhau bên bờ là đường thẳng d. Đường thẳng MN cắt AO và AC lần lượt tại H và K.
a, Chứng minhAM bình AH.AO
b, Gọi I là trung điểm của BC. Chứng minh góc AMK góc AIN
c, Chứng minh rằng đường tròn ngoại tiếp tam giác OHK lun đi qua 1 điểm cố định...
Đọc tiếp
Cho đường tròn tâm O điểm A nằm ngoài đường tròn. Vẽhai tiếp tuyến AM, AN với đường tròn tâm O ( M,N là hai tiếp điểm). Qua A vẽ 1 đường thẳng d cắt đường tròn tâm O tại B và C sao cho 2 điểm nằm giữa A và C, hai điểm O và N nằm trên hai nửa mặt phẳng đối nhau bên bờ là đường thẳng d. Đường thẳng MN cắt AO và AC lần lượt tại H và K.
a, Chứng minhAM bình = AH.AO
b, Gọi I là trung điểm của BC. Chứng minh góc AMK= góc AIN
c, Chứng minh rằng đường tròn ngoại tiếp tam giác OHK lun đi qua 1 điểm cố định khi đường tròn tâm O thay đổi nhưng lun đi qua điểm B và C cố định
cho nửa đường tròn (o; ab)c là điểm nằm giữa o và a ,đường thẳng vuông góc với ab . tại c cắt nửa đường tròn tại i , k là điểm bất kỳ nằm trên đoạn thẳng ci (k khác c và i) , tia ak cắt nửa đường tròn (o) tại m, tia bm cắt tia ci tại d. chứng minh: a, các tứ giác acmd, bckm nội tiếp đường tròn. b, ck.cd ca.cb. c, gọi n là giao điểm của ad và đường tròn (o) chứng minh b,k,n thẳng hàng
Đọc tiếp
cho nửa đường tròn (o; ab)c là điểm nằm giữa o và a ,đường thẳng vuông góc với ab . tại c cắt nửa đường tròn tại i , k là điểm bất kỳ nằm trên đoạn thẳng ci (k khác c và i) , tia ak cắt nửa đường tròn (o) tại m, tia bm cắt tia ci tại d. chứng minh: a, các tứ giác acmd, bckm nội tiếp đường tròn. b, ck.cd = ca.cb. c, gọi n là giao điểm của ad và đường tròn (o) chứng minh b,k,n thẳng hàng
a) Xét (O) có
ΔAMB nội tiếp đường tròn(A,M,B\(\in\)(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
\(\Leftrightarrow AM\perp MB\) tại M
\(\Leftrightarrow AM\perp BD\) tại M
\(\Leftrightarrow\widehat{AMD}=90^0\)
Xét tứ giác ADMC có
\(\widehat{AMD}=\widehat{ACD}\left(=90^0\right)\)
\(\widehat{AMD}\) và \(\widehat{ACD}\) là hai góc cùng nhìn cạnh AD
Do đó: ADMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O), đường kính AB và một điểm C nằm trên nửa đường tròn. Gọi D là một điểm nằm trên đường kính AB, qua D kẻ đường vuông góc với AB, cắt BC tại F, cắt AC tại E. Tiếp tuyến của nửa đường tròn tại C cắt EF tại I. c/m
a) I là trung điểm EF
b) OC là tiếp tuyến của (ECF)
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
=>BC\(\perp\)AC tại C
=>BC\(\perp\)AE tại C
=>ΔCEF vuông tại C
Xét (O) có
\(\widehat{ICB}\) là góc tạo bởi tiếp tuyến CI và dây cung CB
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
Do đó: \(\widehat{ICB}=\widehat{CAB}\)
mà \(\widehat{CAB}=\widehat{BFD}\left(=90^0-\widehat{CBA}\right)\)
nên \(\widehat{ICB}=\widehat{BFD}\)
mà \(\widehat{BFD}=\widehat{IFC}\)(hai góc đối đỉnh)
nên \(\widehat{ICB}=\widehat{IFC}\)
=>\(\widehat{ICF}=\widehat{IFC}\)
=>IC=IF
Ta có: \(\widehat{ICF}+\widehat{ICE}=\widehat{ECF}=90^0\)
\(\widehat{IFC}+\widehat{IEC}=90^0\)(ΔECF vuông tại C)
mà \(\widehat{ICF}=\widehat{IFC}\)
nên \(\widehat{ICE}=\widehat{IEC}\)
=>IC=IE
mà IC=IF
nên IE=IF
=>I là trung điểm của EF
b: Vì ΔCEF vuông tại C
nên ΔCEF nội tiếp đường tròn đường kính EF
=>ΔCEF nội tiếp (I)
Xét (I) có
IC là bán kính
OC\(\perp\)CI tại C
Do đó: OC là tiếp tuyến của (I)
Đúng 1
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB, C là một điểm nằm trên đường tròn ( C khác A,B) (BC
Cho nửa đường tròn(o) đường kính AB và điểm M nằm trên nửa đường tròn đó. Kẻ MH vuông góc AB và BH nằm trong nửa đường tròn(o), MA,MB cắt các nửa đường tròn trên lần lượt tai P và Q. Chứng minh rằng a) PQMH b)MP.MAMQ.MB c)PQ là tiếp tuyến chung của hai nửa đường tròn d) tứ giác ABQP nội tiếp đường tròn e) xác định vị trí của M trên nửa đường tròn(o) để tứ giác MPHQ là hình vuông
Đọc tiếp
Cho nửa đường tròn(o) đường kính AB và điểm M nằm trên nửa đường tròn đó. Kẻ MH vuông góc AB và BH nằm trong nửa đường tròn(o), MA,MB cắt các nửa đường tròn trên lần lượt tai P và Q. Chứng minh rằng a) PQ=MH b)MP.MA=MQ.MB c)PQ là tiếp tuyến chung của hai nửa đường tròn d) tứ giác ABQP nội tiếp đường tròn e) xác định vị trí của M trên nửa đường tròn(o) để tứ giác MPHQ là hình vuông
Giải hộ mình bài này nhé. Mình cần RẤT GẤP!!!!!!! : Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh: a) Tứ giác ACMD, BCKM nội tiếp đường tròn. b) CK.CDCA.CB c) Gọi giao điểm của AD và nửa đường tròn (O) là N. Chứng minh B,K,N thẳng hàng. d) Tâm đường tròn ngoại tiếp tam giác AKD...
Đọc tiếp
Giải hộ mình bài này nhé. Mình cần RẤT GẤP!!!!!!! : Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh: a) Tứ giác ACMD, BCKM nội tiếp đường tròn. b) CK.CD=CA.CB c) Gọi giao điểm của AD và nửa đường tròn (O) là N. Chứng minh B,K,N thẳng hàng. d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI.
Bài 1: Cho nửa đường tròn tâm O đường kính AB. Kẻ tiếp tuyến Ax và By với nửa đường tròn. Từ một điểm C trên nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax và By ở P và Q. a) Chứng minh rằng: Bốn điểm O, A, P, C cùng nằm trên một đường tròn. b) AC cắt OP tại M, OQ cắt CB tại N. Chứng minh tứ giác ONCM là hình chữ nhật. c) Chứng minh PA . BQ OB . OA d) Chứng minh AB là tiếp tuyến của đường tròn đường kính PQ. các bn giúp mik với:(((
Đọc tiếp
Bài 1: Cho nửa đường tròn tâm O đường kính AB. Kẻ tiếp tuyến Ax và By với nửa đường tròn. Từ một điểm C trên nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax và By ở P và Q. a) Chứng minh rằng: Bốn điểm O, A, P, C cùng nằm trên một đường tròn. b) AC cắt OP tại M, OQ cắt CB tại N. Chứng minh tứ giác ONCM là hình chữ nhật. c) Chứng minh PA . BQ = OB . OA d) Chứng minh AB là tiếp tuyến của đường tròn đường kính PQ. các bn giúp mik với:(((
a: Xét tứ giác OAPC có
góc OAP+góc OCP=180 độ
nên OAPC là tứ giác nội tiếp
b: Xét (O) có
PC,PA là tiếp tuyến
nên PA=PC
mà OC=OA
nên OP là trung trực của AC
=>OP vuông góc với AC
Xét (O) có
QC,QB là các tiếp tuyến
nên QC=QB
mà OB=OC
nên OQ là trung trực của BC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đo: ΔACB vuông tại C
Xét tứ giác CMON có
góc CMO=góc CNO=góc MCN=90 độ
nen CMON là hình chữ nhật
c: PA*BQ=PC*CQ=OC^2=OB*OA
Đúng 0
Bình luận (0)