giải phương trình
a, x5 + xx4 + x3 + x2 + x + 1 =0
b, x5-x4+3x3+3x2- x +1=0
Bài 1: Giải phương trình:
a) ( x+1)2 (x+2) + ( x – 1)2 ( x- 2) = 12
b) x4 + 3x3 + 4x2 + 3x + 1 = 0
c) x5 – x4 + 3x3 + 3x2 –x + 1 = 0
Bài 2: Chứng minh rằng các phương trình sau vô nghiệm
a) x4 – x3 + 2x2 – x + 1 = 0
b) x4 + x3 + x2 + x + 1 = 0
c) x4 – 2x3 +4x2 – 3x +2 = 0
d) x6+ x5+ x4 + x3 + x2 + x + 1 = 0
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
2.
a. \(x^4-x^3+x^2+x^2-x+1=0\)
\(\Leftrightarrow x^2\left(x^2-x+1\right)+x^2-x+1=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\left(vn\right)\\x^2-x+1=0\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\left(vn\right)\end{matrix}\right.\)
Vậy pt vô nghiệm
b.
\(x^4+x^3+x^2+x+1=0\)
\(\Leftrightarrow x\left(x^3+1\right)+x^3+1+x^2=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^3+1\right)+x^2=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x^2-x+1\right)+x^2=0\)
Mà \(\left\{{}\begin{matrix}\left(x+1\right)^2\left(x^2-x+1\right)\ge0\\x^2\ge0\end{matrix}\right.\)
Nên dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\) ko tồn tại x thỏa mãn
Nghiệm của phương trình x 5 - x 4 + 3 x 3 + 3 x 2 - x + 1 = 0 là:
A. x = 1
B. x = -1
C. x = ± 1
D. x = 3
Tính f(x) + g(x) với:
f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
= x5 – (3x2 + x2 ) + x3 - 2x + 5
= x5 – 4x2 + x3 – 2x + 5
= x5 + x3 – 4x2 – 2x + 5
Và g(x) = x2 – 3x + 1 + x2 – x4 + x5
= (x2 + x2 ) – 3x + 1 – x4 + x5
= 2x2 – 3x + 1 – x4 + x5
= x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
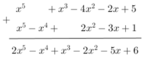
Tính f(x) - g(x) với:
f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5
giúp với ạ
\(f\left(x\right)-g\left(x\right)=\left(x^5-3x^2+x^3-x^2-2x+5\right)-\left(x^2-3x+1+x^2-x^4+x^5\right)\)
\(f\left(x\right)-g\left(x\right)=x^5-3x^2+x^3-x^2-2x+5-x^2+3x-1-x^2+x^4-x^5\)
\(f\left(x\right)-g\left(x\right)=\left(x^5-x^5\right)+\left(-3x^2-x^2-x^2-x^2\right)+x^3+\left(-2x+3x\right)+\left(5-1\right)+x^4\)
\(f\left(x\right)-g\left(x\right)=-6x^2+x^3+x+4+x^4\)
\(f\left(x\right)-g\left(x\right)=x^4+x^3-6x^2+x+4\)
Gpt: x5-x4+3x3+3x2-x+1=0
Ta có: \(x^5-x^4+3x^3+3x^2-x+1=0\)
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow x+1=0\)
hay x=-1
Câu 1 (3,0 điểm): Tính
a) 3x2 (2x2 − 5x − 4)
b) (x + 1)2 + ( x − 2 )(x + 3 ) − 4x
c) (6 x5 y2 − 9 x4 y3 +12 x3 y4 ) : 3x3 y2
Câu 2 (4,0 điểm): Phân tích đa thức thành nhân tử
a) 7x2 +14xy b) 3x + 12 − (x2 + 4x)
c ) x2 − 2xy + y2 − z2 d) x2 − 2x −15
Câu 3 (0,5 điểm): Tìm x
a) 3x2 + 6x = 0 b) x (x − 1) + 2x − 2 = 0
Câu 4 (2,0 điểm): Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh DE song song BF
b) Tứ giác DEBF là hình gì?
Câu 5 (0,5 điểm ):
Chứng minh rằng A= n3 + (n+1)3 + (n+2)3 chia hết cho 9 với mọi n ∈ N*
\(1,\\ a,=6x^4-15x^3-12x^2\\ b,=x^2+2x+1+x^2+x-3-4x=2x^2-x-2\\ c,=2x^2-3xy+4y^2\\ 2,\\ a,=7x\left(x+2y\right)\\ b,=3\left(x+4\right)-x\left(x+4\right)=\left(3-x\right)\left(x+4\right)\\ c,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ d,=x^2-5x+3x-15=\left(x-5\right)\left(x+3\right)\\ 3,\\ a,\Leftrightarrow3x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Câu 1
a)\(3x^2\left(2x^2-5x-4\right)=6x^4-15x^3-12x^2\)
b)\(\left(x+1\right)^2+\left(x-2\right)\left(x+3\right)-4x=x^2+2x+1+x^2+3x-2x-6-4x=2x^2-x-5\)
Bài 2
a) \(7x^2+14xy=7x\left(x+2y\right)\)
b) \(3x+12-\left(x^2+4x\right)=-x^2-x+12=\left(-x+3\right)\left(x+4\right)\)
c) \(x^2-2xy+y^2=\left(x-y\right)^2\)
d) \(x^2-2x-15=x^2+3x-5x-15=\left(x+3\right)\left(x-5\right)\)
giải phương trình sau:
a. (9x2-4)(x+1) = (3x+2) (x2-1)
b. (x-1)2-1+x2 = (1-x)(x+3)
c. (x2-1)(x+2)(x-3) = (x-1)(x2-4)(x+5)
d. x4+x3+x+1=0
e. x3-7x+6 = 0
f. x4-4x3+12x-9 = 0
g. x5-5x3+4x = 0
h. x4-4x3+3x2+4x-4 = 0
m.n jup vs
Cau 1:
Tim x, biet: 1-4+7-10+.............-x=-75
Cau 2:
Cho x1, x2, x3, x4, x5 thuộc Z
Biết x1+ x2 + x3 + x4 + x5=0
và x1 + x2=x3+ x4= x4 + x5 =2
Tinh x3, x4 , x5
Cau 3: Tim x biet
(x+7+1) chia het cho (x+7)
Cho đa thức
F(x)=x5 - 3x2 -x3 - x2 - 2x + 5
G(x)+x5 - x4 + x2 - 3x + x2 + 1
Tính H(x) = F(x) + G(x)
\(H\left(x\right)=F\left(x\right)+G\left(x\right)=\left(x^5-3x^2-x^3-x^2-2x+5\right)+\left(x^5-x^4+x^2-3x+x^2+1\right)\\ =x^5-3x^2-x^3-x^2-2x+5+x^5-x^4+x^2-3x+x^2+1\\ =\left(x^5+x^5\right)-x^4-x^3-\left(3x^2+x^2-x^2-x^2\right)-\left(2x+3x\right)+5\\ =2x^5-x^4-x^3-2x^2-5x+5\)
Tính f(x) + g(x) với:
f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5 = x5 + x3 – 4x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5 = x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5 = x5 + x3 – 4x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5 = x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x): tự làm nha bạn