Cho hình vuông ABCD. Vẽ hình tròn (O) đường kình AD và đường tròn (C;CB). Cúng cắt nhau tại điểm E (khác điểm D). Tia AE cắt BC tại F
Chứng minh tứ giác OAFC là hình bình hành từ đó suy ra F là trung điểm của BC
Cho hình vuông ABCD. Vẽ hình tròn (O) đường kình AD và đường tròn (C
C;CB). Chúng cắt nhau tại điểm E (khác điểm D). Tia AE cắt BC tại F
a)CM:AFCD là hbh
b)CM;F là trung đ BC
c) Cho AB=a,Tính S AFCD
Cho hình tròn tâm O và hai đường kình AB và BD vuông góc với nhau. Biết diện tích hình vuông ABCD là 120 cm vuông. Tính diện tích hình tròn tâm O
gọi cạnh hình vuông là a. diện tích hình vuông là \(a^2\)=120cm
xét tam giác OAB vuông cân tại O (OA=OB=bán kính=R)
AD ĐL Py-ta-go : \(AB^2\)=\(OA^2\)+\(OB^2\) => \(a^2=R^2+R^2\)\(=2R^2\) => \(R^2=\frac{a^2}{2}\Rightarrow R^2=\frac{120}{2}=60cm\)
Vậy, diện tích hình tròn cần tìm là : \(S_{hinhtron}=\pi R^2=\pi.60=60\pi\)\(cm^2\)
chỗ đơn vị của \(a^2\) và \(R^2\) em sửa thành \(cm^2\) nha em.
vẽ hình hộ mình đề này Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK= AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
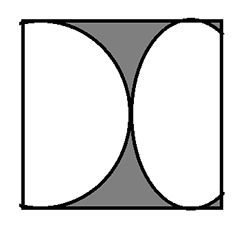
Cho hình vuông ABCD. Vẽ 2 nửa hình tròn đường kính AD, BC (bạn tự hình dung nhé). Biết chu vi đường tròn đường kính AD - 25,12cm. Tính diện tích phần tô đậm.
| Nhật Tân |
| Chủ nhật, ngày 28/01/2018 06:13:29 |

cho hình vuông abcd có 2 đường chéo ac và bd vuông góc với nhau và bằng 12 cm, 2 đường chéo này cắt nhau tại o. từ o ta vẽ 1 hình tròn có đường kính bằng cạnh hình vuông abcd
tính diện tích hình tròn này
Cho hình vuông ABCD có cạnh là 10cm.M và N lần lượt là các điểm chính giữa AD và BC.Lấy MN làm đường kính vẽ đường tròn tâm O.Hỏi diện tích hình vuông hơn diện tích hình tròn bao nhiêu xăng-ti-mét vuông?
Cho hình vuông ABCD có 2 đường chéo AC và BD , vuông góc với nhau tại O. Lấy O làm tâm vẽ 1 hình tròn có đường kính = cạnh hình vuông, biết đường chéo hình vuông là `12 cm. Tinh điện tích hình tròn
cho hình vuông ABCD , hai đường chéo cắt nhau tại điểm O . lấy O làm tâm vẽ đường tròn đi qua các điểm A, B,C,D . biết hình tròn có diện tích 50,24 cm2 . hãy tính diện tích hình vuông ABCD
ta thấy OA = OB =OC=OD = bán kính của hình tròn .
bán kính * bán kính hình tròn là :
50,24 : 3,14 = 16 ( cm )
mà 16 = 4* 4 => bán kính hình tròn = 4cm.
diện tích hình tam giác AOB là :
4 * 4 : 2 = 8 ( cm2 )
diện tích hình vuông ABCD là :
8 4 = 32 ( cm2 )
đáp số : 32 cm2
nếu biết trước đáp án là vậy
thì đừng hỏi khỏi tốn thời gian
lấy ít phút đi giải bài khác
được l-i-k-e nhiều khỏi tốn iQ
Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK= AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
a: Xét (O) có
AD là đường kính
AB\(\perp\)AD tại A
Do đó: AB là tiếp tuyến của (O)
Xét tứ giác AOMB có \(\widehat{OAB}+\widehat{OMB}=90^0+90^0=180^0\)
nên AOMB là tứ giác nội tiếp
=>A,O,M,B cùng thuộc một đường tròn
b: Xét (O) có
OD là bán kính
DK\(\perp\)DO tại D
Do đó: DK là tiếp tuyến của (O)
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: OB là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOB}\)
Xét (O) có
KM,KD là các tiếp tuyến
Do đó: OK là phân giác của góc DOM
=>\(\widehat{DOM}=2\cdot\widehat{KOM}\)
Ta có: \(\widehat{MOA}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{KOM}+\widehat{BOM}\right)=180^0\)
=>\(2\cdot\widehat{KOB}=180^0\)
=>\(\widehat{KOB}=90^0\)
=>OK\(\perp\)OB
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: BA=BM
Xét (O) có
KD,KM là các tiếp tuyến
Do đó: KD=KM
Xét ΔOBK vuông tại O có OM là đường cao
nên \(BM\cdot MK=OM^2\)
=>\(BM\cdot MK=\left(\dfrac{1}{2}AD\right)^2=\dfrac{1}{4}AD^2=\dfrac{1}{4}AB^2\)
c: Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM
mà BO\(\perp\)OK
nên AM//OK
Xét ΔDEA có
O là trung điểm của AD
OK//AE
Do đó: K là trung điểm của DE