BÀI 6.Chứng minh rằng qua ba điểm không thẳng hàng ta vẽ được một và chỉ mộtđường tròn. Với ba điểm thẳng hàng thì kết luận sẽ như thế nào? Vì sao?

Những câu hỏi liên quan
giúp e ạ
Chứng minh rằng qua ba điểm không thẳng hàng ta vẽ được một và chỉ mộtđường tròn. Với ba điểm thẳng hàng thì kết luận sẽ như thế nào? Vì sao?
Qua 3 điểm không thẳng hàng chỉ vẽ được một và chỉ một tam giác, từ đó suy ra chỉ vẽ được một và chỉ một đường tròn ngoại tiếp qua tam giác đó hay chỉ vẽ được một và chỉ một đường tròn đi qua 3 điểm không thẳng hàng
Với 3 điểm thẳng hàng thì sẽ không dựng được tam giác nên sẽ không vẽ được đường tròn đi qua 3 điểm đó
Đúng 1
Bình luận (0)
Với 3 điểm không thẳng hàng sẽ tạo ra được 1 tam giác . Bằng việc vẽ đường trung trực của 2 đoạn , ta sẽ tìn được tâm của tam giác đó ( đi qua 3 điểm không thẳng hàng )
Tương tự như vậy , nếu có 1 đường tròn đi qua 3 điểm thẳng hàng thì ta có thể xác định tâm của đường tròn đó bằng cách xđ giao điểm của 3 đường trung trực
Theo hình vẽ thì 2 đường trung trực song song vs nhau
=> Ko có đường tròn nào đi qua 3 điểm thẳng hàng
Đúng 0
Bình luận (0)
Qua ba điểm không thẳng hàng ta chỉ xác định được một đường tròn.
Thế còn qua ba điểm thẳng hàng thì sao ạ
thì xác định được ba điểm nằm cùng trên một đoạn thẳng
Đúng 0
Bình luận (1)
Qua ba điểm không thẳng hàng ta chỉ xác định được một đường tròn.
Thế còn qua ba điểm thanwge hàng thì sao ạ
xác định được ba điểm nằm trên một đường thẳng
Đúng 0
Bình luận (0)
cho 20 điểm trong đó không có ba điểm nào thẳng hàng . Cứ qua 2 điểm ta vẽ được 1 đường thẳng .Hỏi vẽ được bao nhiêu đường thẳng ? vì sao?
b, cho n điểm trong đó không có ba điểm nào thẳng hàng . Cứ qua 2 điểm ta vẽ được 1 đường thẳng . Biết rằng có tất cả 105 đường thẳng . Tính n
Ta chọn 1 điểm bất kì,qua điểm đó ta nối lần lượt với 19 điểm còn lại ta vẽ được 19 đường thẳng.
Như vậy ta sẽ được 19x20 nhưng mỗi đường thẳng đã được tính hai lần do đó có tất cả:
(20x19):2=190 đường thẳng
Vậy vẽ được 190 đường thẳng
Đúng 0
Bình luận (0)
Bài 9. Cho 11 điểm đôi một phân biệt thoả mãn:
i) Không có ba điểm nào thẳng hàng;
ii) Không có bốn điểm nào cùng nằm trên một đường tròn.
Chứng minh rằng có thể vẽ được một đường tròn đi qua ba điểm trong các điểm đã cho và chứa đúng 6 điểm bên trong.
Vẽ ba điểm A B C không thẳng hàng .Qua A vẽ đường thẳng d1 và d2 sao cho d1 vuống với BC và d2 song song với BC .Có kết luận gì về đường thẳng d1 và d2 .Vì sao?
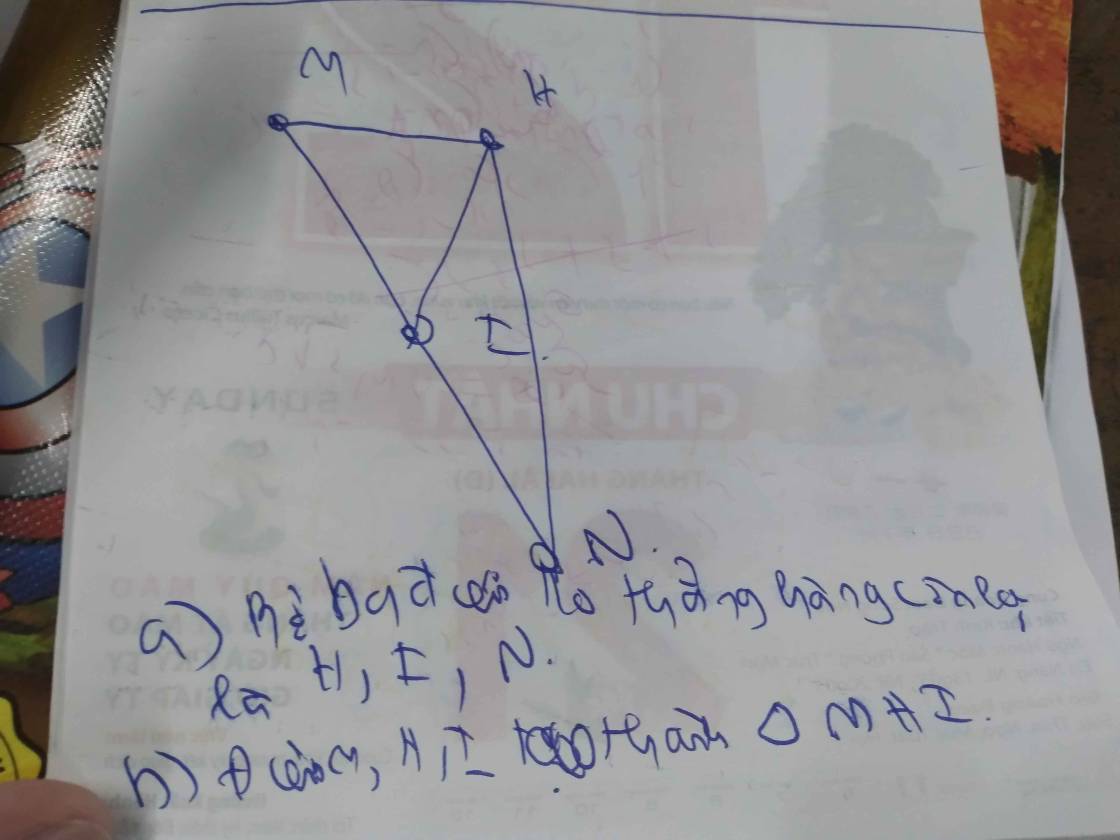
Vẽ ba điểm M,H,I không thẳng hàng.Vẽ tiếp điểm N sao cho M,N,I thẳng hàng và I nằm giữa M và N
a)Tìm bộ ba điểm không thẳng hàng còn lại?
b)Điểm I và N như thế nào với điểm N?Điểm M,H như thế nào với điểm I
cho trước 6 điểm. vẽ các đường thẳng đi qua các cặp điểm
a) nếu trong 6 điểm đó không có ba điểm nào thẳng hàng thì sẽ vẽ được bao nhiêu đường thẳng?
b) nếu trong 6 điểm đó có đúng 3 điểm thẳng hàng thì sẽ vẽ được bao nhiêu đường thẳng?
a,nếu trong 6 điểm ko có 3 điểm nào thẳng hàng thì vẽ được:6.(6-1)/2=15 đường thẳng
b,ta chia 6 điểm thành 2 nhóm :
nhóm 1:3 điểm thẳng hàng ta vẽ được 1 đường thẳng
nhóm 2 : 3 điểm còn lại vẽ được 1 đường thẳng
cứ 1 diểm của nhóm 1 nối với 1 điểm của nhóm 2 thì vẽ được 3 đường thẳng.vậy với 3 điểm của nhóm 1 nối với 3 điểm của nhóm 2thì ta được 3.3=9 đường thẳng
mình chắc chắn là đúng
chúc bạn học tốt
Đúng 0
Bình luận (0)
mình trả lời thiếu cho mình bổ sung
vậy có 9+2=11 đường thẳng
Đúng 0
Bình luận (0)
a, Nếu trong 6 điểm không có 3 điểm nào thẳng hàng thì viết được :
6 * (6 - 1) / 2 = 15 ( đường thẳng )
b, Ta chia 6 điểm thành 2 nhóm :
Nhóm 1 : 3 điểm thẳng hàng ta viết được 1 đường thẳng.
Nhóm 2 : 3 điểm còn lại vẽ được 1 đường thẳng.
Cứ 1 điểm của nhóm 1 nối với 1 điểm của nhóm 2 thì viết được 3 đường thẳng. Vậy với 3 điểm của nhóm 1 nối với 3 điểm của nhóm 2 thì ta được :
3 * 3 = 9 (đường thẳng)
Đ/s : 9 đường thẳng.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho bốn điểm A, B, C và D phân biệt sao cho không có ba điểm nào thẳng hàng. Hãy tìm điểm M sao cho ba điểm A, B, M thẳng hàng, đồng thời ba điểm C, D và M cũng thẳng hàng. Khi nào thì không thể tìm được điểm M như thế?
Giao điểm của AB và CD chính là điểm M thỏa mãn đề bài.
Một lẽ dĩ nhiên là nếu AB song song với CD thì ta không thể tìm được giao điểm của chúng, dẫn đến không tìm được điểm M theo yêu cầu.