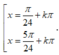Giải phương trình :
\(2sin3x+3cos3x=-2\)
Những câu hỏi liên quan
Giải phương trình: Sin2x.Cosx + √3cos3x= √3-cos2x.sinx
Giải phương trình
4
sin
3
x
+
3
cos
3
x
-
3
sin
x
-
sin
2
x
cos
x
0
Đọc tiếp
Giải phương trình 4 sin 3 x + 3 cos 3 x - 3 sin x - sin 2 x cos x = 0
Giải các phương trình
g
(
x
)
0
v
ớ
i
g
(
x
)
sin
3
x
-
3
cos
3
x
+
3
cos
x
-
...
Đọc tiếp
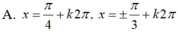
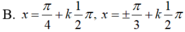
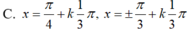
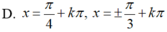
Giải các phương trình g ' ( x ) = 0 v ớ i g ( x ) = sin 3 x - 3 cos 3 x + 3 cos x - 3 sin x
Giải phương trình sau:
a)sinx+\(\sqrt{3}cosx=2sin3x\)
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=sin3x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin3x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+\dfrac{\pi}{3}+k2\pi\\3x=\dfrac{2\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
Đúng 1
Bình luận (3)
Giải phương trình sin3x(cosx - 2sin3x) + cos3x(1 + sinx - 2cos3x) 0 A. x ±
π
3
+ k2π, k ∈ Z B. x
π
4
+ kπ, k ∈ Z C. x
-
π
4
+ k2π, x
-
π
6
+ k2π,k ∈ Z D. Vô nghiệm
Đọc tiếp
Giải phương trình sin3x(cosx - 2sin3x) + cos3x(1 + sinx - 2cos3x) = 0
A. x = ± π 3 + k2π, k ∈ Z
B. x = π 4 + kπ, k ∈ Z
C. x = - π 4 + k2π, x = - π 6 + k2π,k ∈ Z
D. Vô nghiệm
Nghiệm của phương trình
sin
3
x
+
3
cos
3
x
–
3
sin
x
cos
2
x
–
sin
2
x
cos
x
0
là: A.
±
π
3
+
k
π
,
k
∈
ℤ
...
Đọc tiếp
Nghiệm của phương trình sin 3 x + 3 cos 3 x – 3 sin x cos 2 x – sin 2 x cos x = 0 là:
A. ± π 3 + k π , k ∈ ℤ h o ặ c π 4 + k π , k ∈ ℤ
B. π 3 + k π , k ∈ ℤ h o ặ c π 4 + k π , k ∈ ℤ
C. - π 3 + k π , k ∈ ℤ h o ặ c π 4 + k π , k ∈ ℤ
D. ± π 3 + k 2 π , k ∈ ℤ h o ặ c π 4 + k 2 π , k ∈ ℤ
Chọn A
Ta có: sin 3 x + 3 cos 3 x – 3 sin x cos 2 x – sin 2 x cos x = 0
Do cosx=0 không là nghiệm của phương trình nên chia hai vế cho cos 3 x ≠ 0 ta được phương trình:
Đúng 0
Bình luận (0)
2sin3x=cosx
phương trình đẳng cấp bậc 2 ạ
cos3x+sin3x=sinx-cosx
2sin3x = cosx (sin2x + cos2x)
⇔ 2sin3x - sin2x cosx - cos3x = 0
+ Xét cosx = 0 ........
+ Xét cosx khác 0 rồi chia cho cos3x rồi đưa về phương trình bậc 3 của tanx
Đúng 1
Bình luận (2)
sin3x + cos3x = sinx - cosx
Nhân cos2x + sin2x là thành câu trên
Đúng 1
Bình luận (0)
Nghiệm của phương trình
sin
x
-
3
cos
x
2
sin
3
x
là A.
x
π
6
+
k
π
hoặc
x
π
6
+
k
2
π
3
k
∈
Z...
Đọc tiếp
Nghiệm của phương trình sin x - 3 cos x = 2 sin 3 x là
A. x = π 6 + k π hoặc x = π 6 + k 2 π 3 k ∈ Z .
B. x = π 3 + k 2 π hoặc x = π 3 + k 2 π k ∈ Z .
C. x = - π 3 + k 2 π hoặc x = 4 π 3 + k 2 π k ∈ Z .
D. x = π 3 + k π 2 k ∈ Z .
Phương trình
2
sin
3
x
+
π
4
1
+
8
sin
2
x
.
cos
2
2
x
có nghiệm là: A. B. C. D.
Đọc tiếp
Phương trình 2 sin 3 x + π 4 = 1 + 8 sin 2 x . cos 2 2 x có nghiệm là:
A.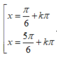 
B.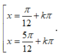 
C.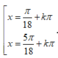 
D. 
