.1.Cho tam giác ABC cân tại A có AD là đường phân giác. a) Chứng minh tam giác ABD tam giác ACDb) Gọi G là trọng tâm tam giác ABC. Chứng minh ba điểm A, G, D thẳng hàng.c) Tính DG biết AB 13cm,BC 10cm2.Cho tam giác ABC vuông ở A, có AB 16cm,AC 30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.3.Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt C ở N. Biết AN MN, BN cắt AM ở O. Chứng minh: a) Tam giác ABC cân ở Ab) O là trọng tâm t...
Đọc tiếp
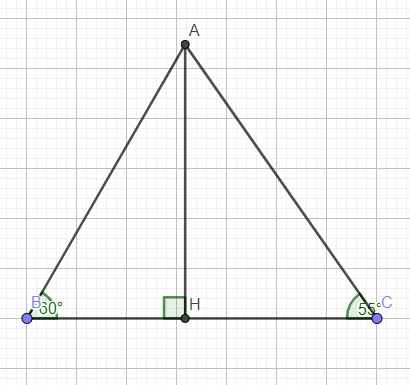
.1.Cho tam giác ABC cân tại A có AD là đường phân giác.
a) Chứng minh tam giác ABD = tam giác ACD
b) Gọi G là trọng tâm tam giác ABC. Chứng minh ba điểm A, G, D thẳng hàng.
c) Tính DG biết AB 13cm,BC 10cm
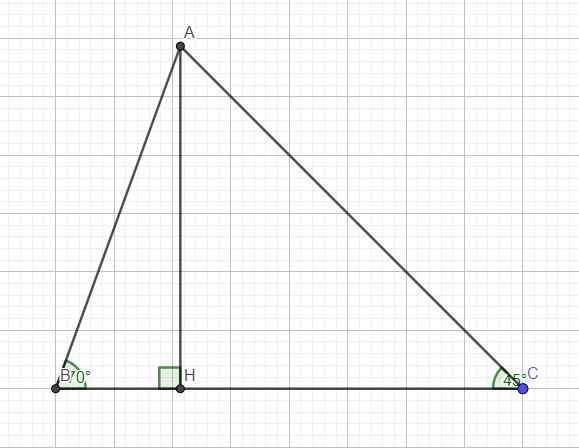
2.Cho tam giác ABC vuông ở A, có AB = 16cm,AC = 30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.
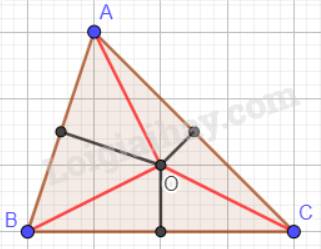
3.Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt C ở N. Biết AN = MN, BN cắt AM ở O. Chứng minh: a) Tam giác ABC cân ở A
b) O là trọng tâm tam giác ABC.
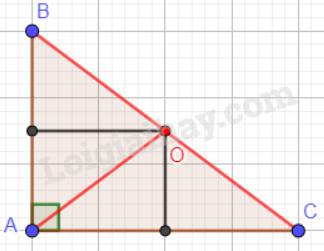
4.Cho tam giác cân ABC, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm O cách đều 3 đỉnh của tam giác ABC.
Cần gấp ạ!