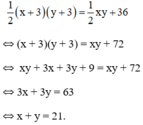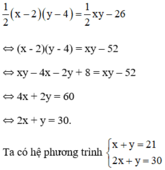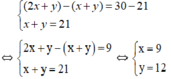Tính độ dài hai cạnh góc vuông của 1 tam giác vuông, biết rằng nếu tăng mỗi cạnh lên 3 cm thì diện tích tam giác đó sẽ tăng thêm 36 cm vuông , và nếu 1 cạnh giảm đi 2 cm , cạnh kia giảm đi 4 Cm thì diện tích của tam giác giảm đi 26 cm vuông.
a. Giải hệ phương trình