Cho ΔABC.M∈BC mà MA = 2MB . N∈AC mà NA = 3NC
Phân tích vecto BC theo vecto BN và Cm
Cho ΔABC.M∈BC mà MA = 2MB . N∈AC mà NA = 3NC
Phân tích vecto BC theo vecto BN và Cm
Cho ΔABC.M∈BC mà MA = 2MB . N∈AC mà NA = 3NC
Phân tích vecto BC theo vecto BN và Cm
Cho \(\Delta\)\(ABC.M\in BC\) \(mà\) MA = 2MB . \(N\in AC\) mà NA = 3NC
Phân tích \(\overrightarrow{BC}\) theo \(\overrightarrow{BN}\) và \(\overrightarrow{CM}\)
Cho tam giác ABC có N thuộc cạnh BC sao cho BN = 2NC . Phân tích vecto AN theo hai vecto AB và vecto AC
\(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=-\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
Bài 1. Cho tam giác ABC , gọi M là điểm trên cạnh BC sao cho MC = 2MB
1) Phân tích vecto AM theo vecto AB, vecto AC
2) Gọi D là trung điểm của AC, phân tích vecto MD theo vecto BA, vecto BC
3) Gọi E là trung điểm của BD . Chứng minh A, E, M thẳng hàng
4) Phân tích vecto BC theo vecto BD, vecto AM
CHo tam giác ABC, M là trung điểm của AC, N thuộc BC; 3 vecto BN=2 vecto NC. phân tích các vecto BM, AN,MN theo vecto AB,AC
\(\overrightarrow{BM}=\dfrac{\overrightarrow{BA}+\overrightarrow{BC}}{2}=\dfrac{\overrightarrow{BA}+\overrightarrow{BA}+\overrightarrow{AC}}{2}=-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}=\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}\)
Cho tam giác ABC, trên đường thẳng AC lấy điểm M sao cho vecto MC = 3 vecto MA Đặt , vecto u = vecto BC , vecto v = vecto BA . Hãy phân tích các vecto BM theo hai vecto u và v.
cho tam gaics ABC trên cạnh AB,AC lần lượt lấy các điểm M,N sao cho MA/MB=x; NA/NC=y. I = CM giao với BN. CMR vecto AI=x(vecto IB)+y(vecto IC)
Trước hết ta chứng minh bổ đề sau:
Bổ đề 1: Cho tam giác ABC và 1 điểm M trên cạnh BC. Khi đó: \(\overrightarrow{AM}=\dfrac{MC}{BC}\overrightarrow{AB}+\dfrac{MB}{BC}\overrightarrow{AC}\)
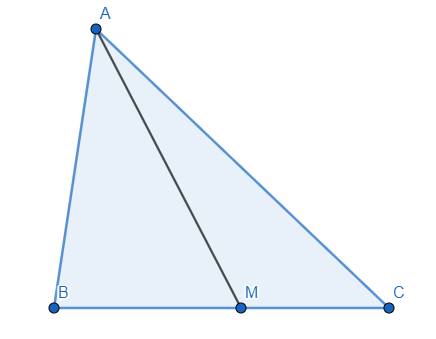
Thật vậy, ta có \(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{BM}{BC}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{BM}{BC}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-\dfrac{BM}{BC}\overrightarrow{AB}\right)+\dfrac{BM}{BC}\overrightarrow{AC}\)
\(=\dfrac{CM}{BC}\overrightarrow{AB}+\dfrac{BM}{BC}\overrightarrow{AC}\), bổ đề 1 được chứng minh.
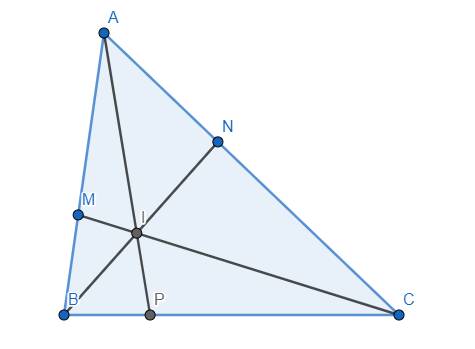
Gọi P là giao điểm của AI và BC. Ta có:
\(\dfrac{MA}{MB}.\dfrac{PB}{PC}.\dfrac{NC}{NA}=1\) \(\Rightarrow x.\dfrac{PB}{PC}.\dfrac{1}{y}=1\) \(\Rightarrow\dfrac{PB}{PC}=\dfrac{y}{x}\) \(\Rightarrow\dfrac{CP}{CB}=\dfrac{x}{x+y}\)
Mặt khác, \(\dfrac{IP}{IA}.\dfrac{MA}{MB}.\dfrac{CB}{CP}=1\) \(\Rightarrow\dfrac{IP}{IA}.x.\dfrac{x+y}{x}=1\) \(\Rightarrow\dfrac{IP}{IA}=\dfrac{1}{x+y}\)
Do đó \(\overrightarrow{AI}=\left(x+y\right)\overrightarrow{IP}\)
Mà theo bổ đề 1: \(\overrightarrow{IP}=\dfrac{PC}{BC}\overrightarrow{IB}+\dfrac{PB}{BC}\overrightarrow{IC}\)
\(=\dfrac{x}{x+y}\overrightarrow{IB}+\dfrac{y}{x+y}\overrightarrow{IC}\)
\(\Rightarrow\overrightarrow{AI}=x\overrightarrow{IB}+y\overrightarrow{IC}\) (đpcm)
cho tam giác ABC .Trên các đường thẳng BC,AC,AB lần lượt lấy các điểm M,N,P sao cho vecto MB=3 vecto MC ,NA= 3vecto CN , vecto PA+vecto PB = vecto 0
a. tính vecto PM,vecto PN theo vecto AB , vecto AC
b. CM :M,N,P thẳng hàng
CẢM ƠN MỌI NGƯỜI