Cho hình chữ nhật ABCD (AB>BC), E là điểm đói xứng với B qua A, F là điểm đối xứng với B qua C.
a. Chứng minh AEDC, ADFC là hình bình hành. b. Chứng minh E đối xứng với F qua D. c. Gọi H là hình chiếu của B trên EF. Từ H kẻ HP vuông góc với AB và HQ vuông góc với BC. Chứng minh BPHQ là hình chữ nhật. d. Chứng minh: BD vuông góc với PQ. e. Chứng minh: AC,BH và PQ đồng quy.
Những câu hỏi liên quan
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với F qua B.
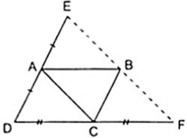
Theo giả thiết ta có:
+ A là trung điểm của DE thì AD = AE ( 1 )
+ C là trung điểm của DF thì CD = CF ( 2 )
Ta có ABCD là hình bình hành nên AD//BC
⇒ AE//BC ( 3 ) và AD = BC ( 4 )
Từ ( 1 ), ( 4 ) ⇒ AE = BC ( 5 )
Từ ( 3 ) và ( 5 ), tứ giác ACBE có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
Áp dụng tính chất và định nghĩa về hình bình hành ACBE ta được 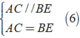
Chứng minh tương tự, tứ giác ACBF là hình bình hành
Ta được: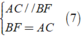
Từ ( 6 ), ( 7 ) ⇒ E, B, F thẳng hàng và BE = BF do đó B là trung điểm của EF hay E đối xứng với F qua B.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Chứng minh: Điểm E đối xứng với điểm F qua điểm B.
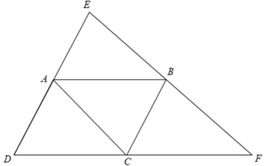
AC là đường trung bình của tam giác Δ DEF
⇒ AC = 1/2EF
+ ABCD là hình bình hành
Mà DC = CF ⇒ AB = 1/2DF.
⇒ AB là đường trung bình của Δ DEF
Do đó B là trung điểm của EF hay E đối xứng với F qua B.
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.
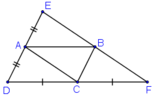
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng điểm E đối xứng với F qua điểm B ?
Bài giải:
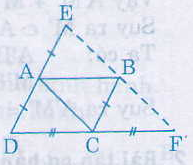
AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B.
Đúng 1
Bình luận (1)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối
xứng với D qua C. Chứng minh rằng E đối xứng với điểm F qua điểm B.
Giải :
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A
⇒ AE = AD
Mà BC = AD
⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
⇒ AEBC là hình bình hành
⇒ EB //= AC (1).
+ F đối xứng với D qua C
⇒ CF = CD
Mà AB = CD
⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
⇒ ABFC là hình bình hành
⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF
⇒ E đối xứng với F qua B
Bài 1.Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, F là điểm đối xứng với D qua C. Chứng minh:
a) AC P EF. b) Điểm E đối xứng với điểm F qua điểm B
Cho hình chữ nhật ABCD ( AB > BC ). Gọi E là điểm đối xứng của B qua A; F là điểm đối xứng của B qua C.
a) Tứ giác ADFC là hình gì? Vì sao?
b) Chứng minh E, D, F thẳng hàng.
c) Chứng minh BDE và BDF có diện tích bằng nhau
vẽ hình làm phần a,b thôi ạ
a: Xét tứ giác ADFC có
AD//FC
AD=FC
=>ADFC là hình bình hành
b: Xét tứ giác AEDC có
AE//DC
AE=DC
=>AEDC là hình bình hành
=>ED//AC
mà AC//DF
nên E,D,F thẳng hàng
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C. Chứng minh rằng điểm E đối xứng với điểm F qua điểm B.

AE // BC (vì AD // BC)
AE = BC (cùng bằng AD)
nên ACBE là hình bình hành.
Suy ra: BE // AC, BE = AC (1)
Tương tự BF // AC, BF = AC (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF. Nên B là trung điểm của EF, vậy E đối xứng với F qua B
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C. Chứng minh rằng
a,AC//EF
b,điểm E đối xứng với điểm F qua điểm B.
AE = AD; AD = BC nên AE = BC(1)
DC = AB; DC = CF nên AB = CF (2)
GÓC EAB = BCF (Đồng vị) (3)
Từ (1); (2); (3) -> tgiac EAB = BCF (cgc) -> EB = BF (*)
Mặt khác: GÓC EBA = EFD (đồng vị); ABC = ADC (gt); CBF = AEB (đồng vị)
Cộng vế với vế: EBA + ABC + CBF = EFD + ADC + AEB
Mà EFD + ADC + AEB = 180 độ -> EBA + ABC + CBF = 180 độ (**)
Từ (*); (**) suy ra điểm E đối xứng với điểm F qua điểm B
Đúng 0
Bình luận (1)
a)
xét tam giácDEF có:
EA=AD
CD=CF
=>AC là đường trung bình của tam giác DEF
=> AC//EF
b)
ta có:
EA=AD
AD=BC
=>EA=BC
EA//BC
=>tứ giác AEBC là hình bình hành
=>EB//AC
EF//AC
=>E,B,F thẳng hàng(1)
xét tam giác AEF và tam giác BCF có:
AE=BC
AB=CF(=DC)
góc A1=góc C1(=góc D1)
=>tam giác AEF=tam giác BCF(c-g-c)
=>EB=BF(2)
từ (1)(2)=>E đới xứng với F qua B(đfcm)
Đúng 1
Bình luận (0)
Các bạn ơi bài này có giải được bằng cách chứng minh phản chứng không vậy?? Nếu được thì chứng minh giúp mình với nhé!!!
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua A, gọi F là điểm đối xứng với D qua C. Chứng minh rằng: điểm E đối xứng với điểm F qua điểm B.
AE = AD; AD = BC nên AE = BC(1)
DC = AB; DC = CF nên AB = CF (2)
GÓC EAB = BCF (Đồng vị) (3)
Từ (1); (2); (3) -> tgiac EAB = BCF (cgc) -> EB = BF (*)
Mặt khác: GÓC EBA = EFD (đồng vị); ABC = ADC (gt); CBF = AEB (đồng vị)
Cộng vế với vế: EBA + ABC + CBF = EFD + ADC + AEB
Mà EFD + ADC + AEB = 180 độ -> EBA + ABC + CBF = 180 độ (**)
Từ (*); (**) suy ra điểm E đối xứng với điểm F qua điểm B.
Đúng 0
Bình luận (0)
Ta có: ABCD là hình bình hành nên AB // CD, AD//BC.
+ E đối xứng với D qua A
=> AE = AD
Mà BC = AD
=> BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE)
=> AEBC là hình bình hành
=> EB // AC (1).
+ F đối xứng với D qua C
=> CF = CD
Mà AB = CD
=> AB = CF
Mà AB // CF (vì AB // CD ≡ CF)
=> ABFC là hình bình hành
=> AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
=> B là trung điểm EF
=> E đối xứng với F qua B






















