
Những câu hỏi liên quan
Cho tam giác ABC vuông ở A.Lấy điểm M nằm trên cạnh BC,hạ MD và ME lần lượt vuông góc với AB và AC (D và E lần nằm trên AB và AC). Lấy điểm I đối xứng với D qua A,K đối xứng với E qua M.a) CM tứ giác DIEK là hình bình hành.b)CM 3 đường thẳng IK,DE,AM giao nhau tại 1 điểmc)Tìm vị trí M trên BC để tứ giác ADME là hình vuôngd)Khi M là chân đường cao hạ từ A xuống BC,gọi J là trung điểm cạnh BC.CMR Ạ vuông góc với DE.Mình cần gấp,xin cảm ơn,giúp mình câu d
Đọc tiếp
Cho tam giác ABC vuông ở A.Lấy điểm M nằm trên cạnh BC,hạ MD và ME lần lượt vuông góc với AB và AC (D và E lần nằm trên AB và AC). Lấy điểm I đối xứng với D qua A,K đối xứng với E qua M.
a) CM tứ giác DIEK là hình bình hành.
b)CM 3 đường thẳng IK,DE,AM giao nhau tại 1 điểm
c)Tìm vị trí M trên BC để tứ giác ADME là hình vuông
d)Khi M là chân đường cao hạ từ A xuống BC,gọi J là trung điểm cạnh BC.CMR Ạ vuông góc với DE.
Mình cần gấp,xin cảm ơn,giúp mình câu d
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB6m;AC8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 24HE mũ 2+4HD mũ 2
Đọc tiếp
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
Cho Tam giác ABC . trên cạnh AB,AC,BC lần lượt lấy các điểm E,D,M sao cho MD//AB và ME//AC gọi I là trung điểm ED
a) Tứ giác AEMD là hình gì
B) Chứng minh rằng điểm A đối xứng với điểm M qua điểm I
a: Xét tứ giác AEMD có
AE//MD
AD//ME
Do đó: AEMD là hình bình hành
Đúng 1
Bình luận (1)
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE. a) Tứ giác ADME là hình gì? Vì sao? b) Chứng minh ba điểm A, I, M thẳng hàng. c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DPDM, EQEM Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
Đọc tiếp
Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE.
a) Tứ giác ADME là hình gì? Vì sao?
b) Chứng minh ba điểm A, I, M thẳng hàng.
c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DP=DM, EQ=EM
Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
Do đó: ADME là hình chữ nhật
b:ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔAMQ có
AE vừa là đường cao, vừa là trung tuyến
=>ΔAMQ cân tại A
=>AE là phân giác của góc MAQ(1)
Xét ΔAMP có
AD vừa là đường cao, vừa là trung tuyến
=>ΔAMP cân tại A
=>AD là phân giác của góc MAP(2)
Từ (1), (2) suy ra góc PAQ=góc MAP+góc MAQ
=2(góc BAM+góc CAM)
=2*góc BAC
=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ=AM
nên A là trung điểm của PQ
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC (A = 90°). Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng với M qua AB và AC. Gọi I, K lần lượt là giao điểm của MẸ với AB và MF với AC. Chứng minh:
a) MIAK là hình chữ nhật.
b) A là trung điểm của EF.
a: M đối xứng E qua AB
=>AB là đường trung trực của ME
=>AB\(\perp\)ME tại I và I là trung điểm của ME
Ta có: M đối xứng F qua AC
=>AC là đường trung trực của MF
=>AC\(\perp\)MF tại K và K là trung điểm của MF
Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
=>AIMK là hình chữ nhật
b: Ta có: AKMI là hình chữ nhật
=>AK//MI và AK=MI; KM//AI và KM=AI
Ta có: MI//AK
I\(\in\)ME
Do đó: IE//AK
Ta có: AK=IM
IM=IE
Do đó: AK=IE
Ta có: AI=MK
MK=KF
Do đó: AI=KF
Ta có: AI//MK
K\(\in\)MF
Do đó: AI//KF
Xét tứ giác AKIE có
AK//IE
AK=IE
Do đó: AKIE là hình bình hành
=>KI//AE và KI=AE
Xét tứ giác AIKF có
AI//KF
AI=KF
Do đó: AIKF là hình bình hành
=>KI//AF và KI=AF
Ta có: KI//AF
KI//AE
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
Ta có: KI=AE
KI=AF
Do đó: AE=AF
mà E,A,F thẳng hàng
nên A là trung điểm của EF
Đúng 1
Bình luận (0)
Cho tam giác ABC và M là trung điểm của BC. Hạ MD, ME theo thứ tự vuông góc với AB và AC. Trên tin BD và CE lần lượt láy các điểm I, K sao cho D là trung điểm của BI, E là trung điểm của CK. Chứng minh 4 điểm B, I, C, K cùng nằm trên một đường tròn
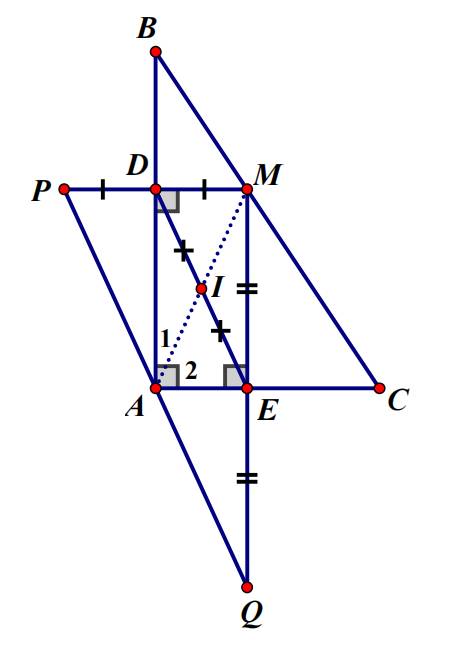
.Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc vớiAB và AC (D thuộc AB, E thuộc AC). Lấy I là trung điểm của DE.a) Tứ giác ADME là hình gì? Vì sao?b) Chứng minh ba điểm A, I, M thẳng hàng.c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho DPDM; EQEM.Chứng minh BA là phân giác của góc MBP và tứ giác BPQC là hình thang.d) Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ.làm câu c,d giúp ạ
Đọc tiếp
.Cho tam giác ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với
AB và AC (D thuộc AB, E thuộc AC). Lấy I là trung điểm của DE.
a) Tứ giác ADME là hình gì? Vì sao?
b) Chứng minh ba điểm A, I, M thẳng hàng.
c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho DP=DM; EQ=EM.
Chứng minh BA là phân giác của góc MBP và tứ giác BPQC là hình thang.
d) Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ.
làm câu c,d giúp ạ
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔBMP có
BD vừa là đường cao, vừa là đường trung tuyến
Do đó: ΔBMP cân tại B
=>BA là phân giác của góc MBP
Xét ΔAMP có
AD là đường cao, là đường trung tuyến
Do đó: ΔAMP cân tại A
=>AB là phân giác của góc MAP(1)
Xét ΔAMQ có
AC vừa là đường cao, vừa là đường trung tuyến
Do đó; ΔAMQ cân tại A
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*góc BAC=180 độ
=>P,A,Q thẳng hàng
Xét ΔAMB và ΔAPB có
AM=AP
AB chung
BM=BP
Do đó: ΔAMB=ΔAPB
=>góc AMB=góc APB
Xét ΔAMC và ΔAQC có
AM=AQ
góc MAC=góc QAC
AC chung
Do đó: ΔAMC=ΔAQC
=>góc AMC=góc AQC
=>góc AQC+góc AMB=180 độ
mà góc AMB=góc APB
nên góc AQC+góc APB=180 độ
=>BP//QC
=>BPQC là hình thang
d: AM=AP
AM=AQ
Do đó: AP=AQ
mà P,A,Q thẳng hàng
nên A là trung điểm của PQ
Đúng 1
Bình luận (0)
1) Cho tam giác cân ABC (ABAC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M,N. DMEN, đường thẳng BC cắt MN tại trung điểm I của MN. Chứng minh rằng: đường thẳng vuông góc vs MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.2)Cho tam giác ABC vuông tại A, K là trung điểm của cạnh BC. Qua K kẻ đường thẳng vuông góc vs AK, đường này cắt các đường thẳng AB và AC lần lượt ở D và E. Gọi...
Đọc tiếp
1) Cho tam giác cân ABC (AB=AC). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M,N. DM=EN, đường thẳng BC cắt MN tại trung điểm I của MN. Chứng minh rằng: đường thẳng vuông góc vs MN tại I luôn đi qua một điểm cố định khi D thay đổi trên cạnh BC.
2)Cho tam giác ABC vuông tại A, K là trung điểm của cạnh BC. Qua K kẻ đường thẳng vuông góc vs AK, đường này cắt các đường thẳng AB và AC lần lượt ở D và E. Gọi I là trung điểm của DE.
a)Chứng minh rằng: AI vuông góc vs BC
b) Có thể nói DE nhỏ hơn BC được không? Vì sao?
3) Cho tam giác ABC (AB>AC), M là trung điểm của BC. Đường thẳng đi qua M và vuông góc vs tia phân giác của góc A tại H cắt hai tia AB, AC lần lượt tại E và F. CMR:
a) EF^2/4 +AH^2=AE^2
b) 2BME=ACB-B
c) BE=CF
4)Cho tam giác ABC có góc B và C là 2 góc nhọn. Trên tia đối của tia AB lấy điểm D sao cho AD=AB, trên tia đối của tia AC lấy điểm E sao cho AE=AC. M là trung điểm của BE, N là trung điểm CB. Ax là tia bất kỳ nằm gưac 2 tia AB và AC. Gọi H, K lần lượt là hình chiếu của B và C trên tia Ax. Xác định vị trí của tia Ax để tổng BH+CK có giá trị lớn nhất.
5)Cho tam giác ABC có 3 góc nhọn, đường cao AH, ở miền ngoài của tam giác ABC ta vẽ các tam giác vuông cân ABE và ACF đều nhận A làm đỉnh góc vuông. Kẻ EM, FN cùng vuông
góc vs AH (M,N thuộc AH)
a) CM: EM+HC=NH
b) CM: EN // FM
bạn đăng từng bài lên 1 đi
mik giải dần cho
Đúng 0
Bình luận (0)
Cho DABC vuông tại C . Trên cạnh AB lấy điểm D sao cho AD = AB. Kẻ qua D đường thẳng vuông góc với AB cắt BC tại E. AE cắt CD tại I.
a) Chứng minh AE là phân giác góc CAB
b) Chứng minh AD là trung trực của CD
c) So sánh CD và BC
d) M là trung điểm của BC, DM cắt BI tại G, CG cắt DB tại K. Chứng minh K là trung điểm của DB.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân ở A,B vuông góc AC tại H. Trên cạnh BC lấy điểm M bất kỳ(M khác B và C). Gọi D;E;F lần lượt là chân đường vuông góc kẻ từ M đến AB;AC và BH.
A) CM: tam giác DBM= tam giác FMB
b) Khi M chạy trên cạnh BC thì tổng MD+ ME không đổi
c) Trên tia đối của tia CA lấy K sao cho KC=EH. CM: BC đi qua trung điểm của DK
Cho tam giác ABC vuông cân tại A , đường trung tuyến AM . Gọi N là điểm đối xứng của A qua M.
a) C/m ABNC là hình vuông.
b) Trên cạnh AB lấy E, trên cạnh AC lấy D sao cho AE=AD. C/m EBCD là hình thang cân.
c) Kẻ AK và DL lần lượt vuông góc với CE ( K và L thuộc BC). Kẻ BI//AK ( I thuộc AC). C/m rằng L đối xứng với B qua K
















