Vẽ (O;R)
a) Vẽ các điểm N,P,Q đều thuộc (O) sao cho điểm P thuộc cung NP
b) Đo và so sánh hai góc \(\widehat{PON}\) và \(\widehat{POQ}\)
c) Cho biết số đo cung nhỏ NQ
Những câu hỏi liên quan
Cho đoạn thẳng OO’ và điểm A nằm giữa hai điểm O và O’. vẽ đường tròn (O; OA) và đường tròn (O’; O’A). Qua A vẽ đường thẳng cắt (O) tại B và cắt (O’) tại C.
a)Chứng minh(O) và (O’) tiếp xúc với nhau.
b)Vẽ đường kính BD của (O) và đường kính CE của (O’). Chứng minh D, A, E thẳng hàng.
Cho điểm A nằm ngoài đường tròn (O), vẽ tiếp tuyến AB của đường tròn (O) (B là tiếp điểm). Vẽ dây BI vuông góc AO tại H, vẽ đường kính BD, tia AD cắt (O) tại E.
a) Chứng minh: AI là tiếp tuyến của (O)
b) Chứng minh: AD.AE=AH.AO
c) Từ O vẽ đường thẳng vuông góc OA cắt AB tại C, vẽ AK vuông góc CD tại K, gọi M là giao điểm của OB và AK. Chứng minh M là trung điểm OB
a: ΔOBI cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOI
Xét ΔOBA và ΔOIA có
OB=OI
góc BOA=góc IOA
OA chung
Do đó: ΔOBA=ΔOIA
=>góc OIA=90 độ
=>AI là tiếp tuyến của (O)
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
gó BAE chung
Do đó: ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE=AH*AO
Đúng 0
Bình luận (0)
vẽ đường tròn tâm O có bán kính OA = 4cm. vẽ điểm C thuộc đường tròn (O) sao cho aÔc = 90'. vẽ tia phân fiacs của góc aOc cắt đường tròn (O) tại D. A)Tính aÔd. B)vẽ tia đối của tia Oa cắt đường tròn (O) tại B . Tính AB và BÔC. C) vẽ bán kính OE trên nữa mặt phẳng bờ AB có chứa điểm C sao cho AÔE = 135'. Hỏi OE có là tia phân giác của góc BOC không? Vì sao?
Vẽ hình vuông ABCD tâm O rồi vẽ tam giác đều có một đỉnh là A và nhận O làm tâm.Nêu cách vẽ
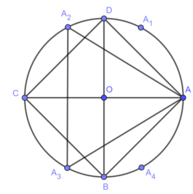
*vẽ hình vuông:
- Vẽ đường tròn (O;R)
- Vẽ hai đường kính AC và BD vuông góc với nhau
- Nối AB ,BC ,CD ,DA ta được tứ giác ABCD là hình vuông nội tiếp trong đường tròn (O;R)
*tam giác đều:
-Từ A đặt liên tiếp các cung bằng nhau và dây căng cung tương ứng có độ dài bằng R:
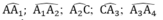
- Nối A A 2 , A 2 A 3 , A 3 A ta được tam giác A A 2 A 3 là tam giác đều nhận O làm tâm
Đúng 0
Bình luận (0)
Vẽ đường tròn tâm O bán kính R=2cm rồi vẽ hình tám cạnh đều nội tiếp đường tròn (O;2cm) .Nêu cách vẽ
- Vẽ đường tròn (O;2cm)
- Vẽ hai đường kính AB và CD vuông góc với nhau
- Nối AB ,BC ,CD ,DA ta được tứ giác ABCD là hình vuông nội tiếp trong đường tròn (O;2cm)
- Vẽ đường kính EF vuông góc với AD ; đường kính GH vuông góc với CD
-Nối AE, ED, DG, GC, CF, FB, BH, HA ta được đa giác AEDGCFBH là đa giác đều tám cạnh nội tiếp trong đường tròn (O;2cm)
Đúng 0
Bình luận (0)
Bài 6.(3,0 điểm) Từ điểmAnằm ngoài đường tròn tâmO, vẽ tiếp tuyếnABvới(O), trong đóBlà tiếp điểm. Vẽ dây cungBCcủa(O)vuông gócvớiOAtạiH.a) Chứng minhAClà tiếp tuyến của(O)vàOB2OH.OA.b) Vẽ cát tuyếnADEvới(O)biết cát tuyến nằm cùng phía vớiBsovới bờOA(Dnằm giữaAvàE). Đường thẳng quaOvuông góc vớiDEtạiKcắtBCtạiM. Chứng minhOK.OMOH.OAvàDMlà tiếp tuyến của(O)
Đọc tiếp
Bài 6.(3,0 điểm) Từ điểmAnằm ngoài đường tròn tâmO, vẽ tiếp tuyếnABvới(O), trong đóBlà tiếp điểm. Vẽ dây cungBCcủa(O)vuông gócvớiOAtạiH.
a) Chứng minhAClà tiếp tuyến của(O)vàOB2=OH.OA.
b) Vẽ cát tuyếnADEvới(O)biết cát tuyến nằm cùng phía vớiBsovới bờOA(Dnằm giữaAvàE). Đường thẳng quaOvuông góc vớiDEtạiKcắtBCtạiM. Chứng minhOK.OM=OH.OAvàDMlà tiếp tuyến của(O)
Vẽ đường tròn tâm O bán kính R = 2cm rồi vẽ hình tám cạnh đều nội tiếp đường tròn (O; 2cm). Nêu cách vẽ ?
Vẽ hình vuông ABCD tâm O rồi vẽ tam giác đều có một đỉnh là A và nhận O làm tâm. Nêu cách vẽ ?
Cho đường thẳng d và điểm O nằm ngoài đường thẳng d. Chỉ sử dụng eke, hãy vẽ đường thẳng d' đi qua O và vuông góc với d. Nói rõ cách vẽ.
Cho đường thẳng d và điểm O thuộc d. Vẽ đường thẳng d' đi qua O và vuông góc với d. Nói rõ cách vẽ và cách sử dụng công cụ ( eke , thước thẳng ) để vẽ.
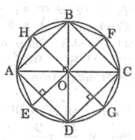
a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).
+ Dựng đoạn thẳng AB = 3cm .
+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.
Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.
b) * Vẽ đường tròn:
Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.
Dựng đường trung trực của đoạn thẳng BC và CA.
Hai đường trung trực cắt nhau tại O.
Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.
* Tính bán kính đường tròn.
+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.
và AA’ ⊥ BC
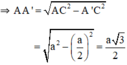
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến
=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến
Suy ra O là trọng tâm tam giác ABC.
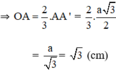
Vậy R = √3 (cm).
c) * Vẽ đường tròn:
Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc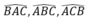 
Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.
Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.
* Tính r:
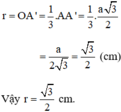
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).
Đúng 0
Bình luận (2)