quy đồng mẫu thức các phân thức :
x+y/ x (y-z)^2 ; y/ x^2 ( y- z) ^2; z/x^2
Những câu hỏi liên quan
Quy đồng mẫu thức các phân thức sau:
\(\dfrac{x+y}{x^{2^{ }}.(y+z)}\); \(\dfrac{y+z}{y^2.\left(z+x\right)}\); \(\dfrac{z+x}{z^2.\left(x+y\right)}\)
\(\dfrac{5x}{x^2+5x+6}\); \(\dfrac{2x+3}{x^2+7x+10}\); -5
Quy đồng mẫu thức ba phân thức :
\(\dfrac{x}{x^2-2xy+y^2-z^2};\dfrac{y}{y^2-2yz+z^2-x^2};\dfrac{z}{z^2-2zx+x^2-y^2}\)
Quy đồng mẫu thức các phân thức sau x x - y ; x+y
MT1: x – y
MT2: 1
MTC: x – y
NTP1: 1; NTP2: x – y.
Quy đồng:
Đúng 0
Bình luận (0)
Quy đồng mẫu thức mỗi phân thức sau:a)
2
x
2
x
3
+
6
x
2
+
12
x
+
8
,
3
x
x...
Đọc tiếp
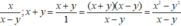
Quy đồng mẫu thức mỗi phân thức sau:
a) 2 x 2 x 3 + 6 x 2 + 12 x + 8 , 3 x x 2 + 4 x + 4 và 5 2 x + 4 với x ≠ − 2 ;
b) x x 2 − 2 xy + y 2 − z 2 , y y 2 − 2 yz + z 2 − x 2 và z z 2 − 2 zx + x 2 − y 2
Với x ≠ y + z ; y ≠ x + z ; z ≠ x + y .
Quy đồng mẫu thức các phân thức sau 1/3x+xy, 2y+2x và 1/x^2+2xy+y^2
\(\dfrac{1}{3x+xy}=\dfrac{1}{x\left(y+3\right)}=\dfrac{\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(2x+2y=2\left(x+y\right)=\dfrac{2\left(x+y\right)\cdot x\left(y+3\right)\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{3x+xy}{x\left(y+3\right)\left(x+y\right)^2}\)
Đúng 2
Bình luận (0)
Quy đồng mẫu thức các phân thức sau: a) 1/x^2y và 3/xy b) x/(x^2+2xy+y^2) và 2x/(x^2+xy)
a: 1/x^2y=1/x^2y
3/xy=3x/x^2y
b: \(\dfrac{x}{x^2+2xy+y^2}=\dfrac{x}{\left(x+y\right)^2}\)
\(\dfrac{2x}{x^2+xy}=\dfrac{2}{x+y}=\dfrac{2x+2y}{\left(x+y\right)^2}\)
Đúng 2
Bình luận (1)
quy đồng mẫu thức các phân thức sau 1/3x+3y, 1/2y+2x và 1/x^2+2xy+y^2
\(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{2\cdot\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{2x+2y}=\dfrac{1}{2\left(x+y\right)}=\dfrac{3\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{1}{\left(x+y\right)^2}=\dfrac{6}{6\left(x+y\right)^2}\)
Đúng 0
Bình luận (1)
1) Cho 2 phân thức :
dfrac{1}{x^2+3x-10};dfrac{x}{x^2+7x+10}
Ko dùng cách phân thức mẫu thức thành nhân tử , hãy chứng tỏ rằng có thể quy đồng mẫu thức 2 phân thức này với mẫu thức chung là : x3 +5x2 - 4x - 20
2) Quy đồng mẫu thức các phân thức :
a) dfrac{x-1}{x^3+1};dfrac{2x}{x^2-x+1};dfrac{2}{x+1}
b) dfrac{x+y}{xleft(y-zright)^2};dfrac{y}{x^2left(y-zright)^2};dfrac{z}{x^2}
Đọc tiếp
1) Cho 2 phân thức :
\(\dfrac{1}{x^2+3x-10};\dfrac{x}{x^2+7x+10}
\)
Ko dùng cách phân thức mẫu thức thành nhân tử , hãy chứng tỏ rằng có thể quy đồng mẫu thức 2 phân thức này với mẫu thức chung là : x3 +5x2 - 4x - 20
2) Quy đồng mẫu thức các phân thức :
a) \(\dfrac{x-1}{x^3+1};\dfrac{2x}{x^2-x+1};\dfrac{2}{x+1}
\)
b) \(\dfrac{x+y}{x\left(y-z\right)^2};\dfrac{y}{x^2\left(y-z\right)^2};\dfrac{z}{x^2}\)
Bài 1 . Chia :( x3 + 5x2 - 4x - 20) cho ( x2 + 3x - 10) ta được x+ 2
Chia :( x3 + 5x2 - 4x - 20) cho ( x2 + 7x + 10) ta được x - 2
Do đó , ta có :
\(\dfrac{1}{x^2+3x-10}=\dfrac{x+2}{\left(x^2+3x-10\right)\left(x+2\right)}=\dfrac{x+2}{x^3+5x^2-4x-20}\)
Và : \(\dfrac{x}{x^2+7x+10}=\dfrac{x\left(x-2\right)}{\left(x^2+7x+10\right)\left(x-2\right)}=\dfrac{x^2-2x}{x^3+5x^2-4x-20}\)
Đúng 0
Bình luận (0)
Bài 2 . a) Ta có :
\(\dfrac{x-1}{x^3+1}\)( giữ nguyên)
\(\dfrac{2x}{x^2-x+1}=\dfrac{2x\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{2x^2+2x}{x^3+1}\)
\(\dfrac{2}{x+1}=\dfrac{2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{2x^2-2x+2}{x^3+1}\)
b) Ta có MTC = x2( y - z)2
Ta có :
\(\dfrac{x+y}{x\left(y-z\right)^2}=\dfrac{x^2+xy}{x^2\left(y-z\right)^2}\)
\(\dfrac{y}{x^2\left(y-z\right)^2}\)( giữ nguyên )
\(\dfrac{z}{x^2}=\dfrac{z\left(y-z\right)^2}{x^2\left(y-z\right)^2}\)
Đúng 0
Bình luận (0)
Tìm mẫu thức chung của các phân thức sau, quy đồng
\(\frac{x}{y^2-yz}\);\(\frac{z}{y^2+yz}\);\(\frac{y}{y^2-z^2}\) . Giúp mk nha mk tik cho. Những người học giỏi toán đâu hết rùi
MTC : \(y^3-z^2y\)
\(\frac{x}{y^2-yz}=\frac{x}{y\left(y-z\right)}=\frac{x\left(y+z\right)}{y\left(y-z\right)\left(y+z\right)}=\frac{xy+xz}{y^3-z^2y}\)
\(\frac{z}{y^2+yz}=\frac{z}{y\left(y+z\right)}=\frac{z\left(y-z\right)}{y\left(y+z\right)\left(y-z\right)}=\frac{yz-z^2}{y^3-z^2y}\)
\(\frac{y}{y^2-z^2}=\frac{y}{\left(y-z\right)\left(y+z\right)}=\frac{y^2}{y^3-z^2y}\)
Đúng 0
Bình luận (0)