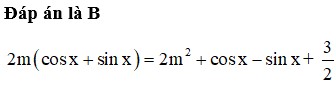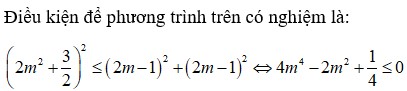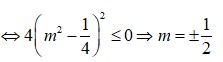Tim tất cả các gia trị của mình để pt cosx+mcos2x=0 có nghiệm

Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để pt có nghiệm :
a. sinx - cosx = m
b. sinx - (2m-1)cosx = m+2
Cho phương trình
sin
x
+
1
sin
2
x
−
m
sin
x
m
cos
2
x
. Tìm tập tất cả các giá trị thực của tham số m để phương trình có nghiệm trên khoảng
0
;...
Đọc tiếp
Cho phương trình sin x + 1 sin 2 x − m sin x = m cos 2 x . Tìm tập tất cả các giá trị thực của tham số m để phương trình có nghiệm trên khoảng 0 ; π 6
A. S = 0 ; 3 2
S. S = 0 ; 1
C. S = 0 ; 1 2
D. S = - 1 ; 3 2
Đáp án A
Phương pháp giải:
Biến đổi công thức lượng giác, đưa phương trình bài cho về dạng phương trình cơ bản, kết hợp với điều kiện nghiệm để tìm giá trị của tham số m
Lời giải:


Đúng 0
Bình luận (0)
Tính tổng tất cả các giá trị \(m\) nguyên để phương trình \(mcos2x=\dfrac{cos^4x-sin^4x}{sinx}\) có đúng 4 nghiệm phân biệt thuộc \(\left(0;2\pi\right)\).
A. 1
B. 2
C. 3
D. 0
Tất cả các giá trị của m để hương trình
cos
x
−
m
0
vô nghiệm là A.
−
1
≤
m
≤
1
B.
m
1
C.
m
−
1
m...
Đọc tiếp
Tất cả các giá trị của m để hương trình cos x − m = 0 vô nghiệm là
A. − 1 ≤ m ≤ 1
B. m > 1
C. m < − 1 m > 1
D. m < − 1
Đáp án là C
phương trình đã cho vô nghiệm khi m > 1
Đúng 0
Bình luận (0)
15. Tìm tất cả các giá trị của tham số m để pt (m -2)sin2x = m +1 vô nghiệm
11. Có tata cả bao nhiêu giá trị nguyên của tham số m để pt √3 . cosx + m -1=0 có nghiệm?
Em vui lòng đăng bài đúng box!
Tìm tất cả các giá trị m để: msinx+cosx=1 có 2 nghiệm thuộc đoạn [0; pi/2]
Xem chi tiết
Đặt \(t=tan\dfrac{x}{2}\Rightarrow\left\{{}\begin{matrix}t\in\left[0;1\right]\\sinx=\dfrac{2t}{1+t^2}\\cosx=\dfrac{1-t^2}{1+t^2}\end{matrix}\right.\)
Pt trở thành: \(\dfrac{m.2t}{1+t^2}+\dfrac{1-t^2}{1+t^2}=1\)
\(\Leftrightarrow2mt+1-t^2=1+t^2\)
\(\Leftrightarrow2mt-2t^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=m\end{matrix}\right.\)
\(\Rightarrow\) Để pt có 2 nghiệm thuộc đoạn đã cho thì \(0< m\le1\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm
2
m
(
c
o
s
x
+
s
i
n
x
)
2
m
2
+
c
o
s
x
-
sin
x
+
3
2
A.
-
1
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm 2 m ( c o s x + s i n x ) = 2 m 2 + c o s x - sin x + 3 2
A. - 1 2 > m < 1 2
B. m = ± 1 2
C. - 1 4 > m < 1 4
D. m = ± 1 4
các ban lm hộ mình bài toán lớp 9 vs
BT1: Tìm tất cả các giá trị của m sao cho PT x^4-4x^3+8x+m=0 có 4 nghiệm phân biệt.
BT2: Cho PT x^2-mx+2m=0. Tìm m để PT sau có 2 nguyeemj phân biệt >2
giải phần b chi tiết
x2-7x+2m+8=0 (1)
a, giải pt m=2
b, tìm tất cả các giá trị của m để pt (1) có 2 nghiệm x1x2
a)Với `m=2` ta có phương trình:
`x^2-7x+2.2+8=0`
`<=>x^2-7x+4+8=0`
`<=>x^2-7x+12=0`
`<=>x^2-3x-4x+12=0`
`<=>(x-3)(x-4)=0`
`<=>[(x=3),(x=4):}`
Vậy với `m=2` thì pt có 2 nghiệm phân biệt là 3 và 4.
`b)` Phương trình có 2 nghiệm `x_1,x_2`
`<=>\Delta>=0`
`<=>7^2-4(2m+8)>=0`
`<=>49-8m-32>=0`
`<=>17>=8m`
`<=>m<=17/8`
Vậy với `m<=17/8` thì pt có 2 nghiệm `x_1,x_2.`
Đúng 1
Bình luận (0)
Lời giải:
a. Khi $m=2$ thì pt trở thành:
$x^2-7x+12=0$
$\Leftrightarrow (x-3)(x-4)=0$
$\Leftrightarrow x-3=0$ hoặc $x-4=0$
$\Leftrightarrow x=3$ hoặc $x=4$
b.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta=49-4(2m+8)\geq 0$
$\Leftrightarrow m\leq \frac{17}{8}$
Đúng 1
Bình luận (0)
a) Thay `m = 2` vào phương trình, ta được:
`x^2 - 7x + 2.2 + 8 = 0`
`<=> x^2 - 7x + 12 = 0`
`<=> x^2 - 3x - 4x + 12 = 0`
`<=> (x^2 - 3x) - (4x - 12) = 0`
`<=> (x-4)(x-3) = 0`
`<=> x - 4 = 0` hoặc `x - 3 = 0`
`<=> x = 4` hoặc `x = 3`
Vậy `m = 2` khi `x = 4` hoặc `x = 3`
`b) x^2 - 7x + 2m + 8 = 0`
`(a = 1; b = -7; c = 2m+8)`
`Δ = b^2 - 4ac = 7^2 - 4 . 1 . (2m+8) = 49 - 8m - 32 = 17 - 8m`
Để phương trình có 2 nghiệm thì `Δ >= 0 <=> 17 - 8m >= 0 <=> 8m <=17 <=> m <= 17/8`
Vậy `m <= 17/8` thì phương trình luôn có `2` nghiệm
Đúng 1
Bình luận (0)