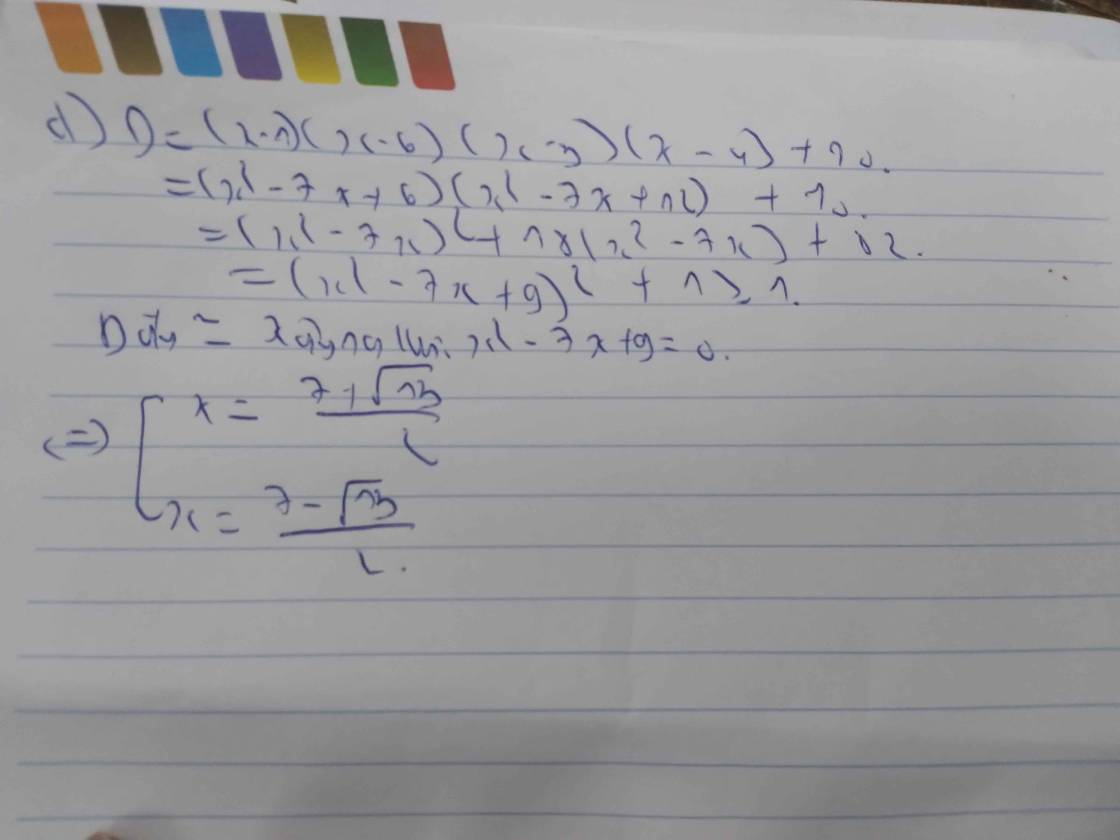\(\left(x^2-4x^2\right)-\left(x-2\right)^2+10.\)

Những câu hỏi liên quan
BT2: Tính giá trị biểu thức
\(M=\left(7-2x\right)\left(4x^2+14x+49\right)-\left(64-8x^3\right)\)tại \(x=1\)
\(P=\left(2x-1\right)\left(4x^2-2x+1\right)-\left(1-2x\right)\left(1+2x+4x^2\right)\)tại \(x=10\)
\(M=\left(7-2x\right)\left(4x^2+14x+49\right)-\left(64-8x^3\right)\)
\(M=\left(7-2x\right)\left[\left(2x\right)^2+2x\cdot7+7^2\right]-\left(64-8x^3\right)\)
\(M=\left[7^3-\left(2x\right)^3\right]-\left(64-8x^3\right)\)
\(M=343-8x^3-64+8x^3\)
\(M=279\)
Vậy M có giá trị 279 với mọi x
\(P=\left(2x-1\right)\left(4x^2-2x+1\right)-\left(1-2x\right)\left(1+2x+4x^2\right)\)
\(P=8x^3-4x^2+2x-4x^2+2x-1-1+8x^3\)
\(P=16x^3-8x^2+4x-2\)
Thay \(x=10\) vào P ta có:
\(P=16\cdot10^3-8\cdot10^2+4\cdot10-2=15238\)
Vậy P có giá trị 15238 tại x=10
Đúng 1
Bình luận (0)
a: M=343-8x^3-64+8x^3=279
b: P=8x^3-4x^2+2x-4x^2+2x-1-1+8x^3
=16x^3-8x^2+4x-2
=16*10^3-8*10^2+4*10-2=15238
Đúng 2
Bình luận (0)
tìm GTLN
a)\(A=x^2+5y^2+2xy-4x-8y+2015\)
b)\(B=\left(x-2012\right)^2+\left(x+2013\right)^2\)
c)\(C=\left(x-1\right)\left(2x-1\right)\left(2x^2-3x-1\right)+2017\)
d)\(D=\left(x-1\right)\left(x-3\right)\left(x-4\right)\left(x-6\right)+10\)
Bạn xem lại đề nhé.
a) \(A=x^2+5y^2+2xy-4x-8y+2015\)
\(A=x^2-4x+4-2y\left(x-2\right)+y^2+2011+4y^2\)
\(A=\left(x-2\right)^2-2y\left(x-2\right)+y^2+2011+4y^2\)
\(A=\left(x-2-y\right)^2+4y^2+2011\)
Vì \(\left(x-y-2\right)^2\ge0;4y^2\ge0\)
\(\Rightarrow A_{min}=2011\)
Dấu bằng xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}x-y-2=0\\4y^2=0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Đúng 0
Bình luận (1)
b) \(B=\left(x-2012\right)^2+\left(x+2013\right)^2\)
\(B=x^2-4024x+2012^2+x^2+4026x+2013^2\)
\(B=2x^2+2x+2012^2+2013^2\)
\(B=2\left(x^2+x+\dfrac{1}{4}\right)+2012^2+2013^2-\dfrac{1}{2}\)
\(B=2\left(x+\dfrac{1}{2}\right)^2+2012^2+2013^2-\dfrac{1}{2}\)
\(\Rightarrow B_{min}=2012^2+2013^2-\dfrac{1}{2}\)
Dấu bằng xảy ra : \(\Leftrightarrow x=-\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Bài 3: Tìm x biết:
1, \(4x^2-36=0\)
2, \(\left(x-1\right)^2+x\left(4-x\right)=11\)
3, \(\left(x-5\right)^2-x.\left(x+2\right)=5\)
4, \(x\left(x+4\right)-x^2-6x=10\)
1: Ta có: \(4x^2-36=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
2: Ta có: \(\left(x-1\right)^2+x\left(4-x\right)=11\)
\(\Leftrightarrow x^2-2x+1+4x-x^2=11\)
\(\Leftrightarrow2x=10\)
hay x=5
Đúng 0
Bình luận (0)
giải pt:
a,\(\left(13-4x\right)\sqrt{2x-3}+\left(4x-3\right)\sqrt{5-2x}=2+8\sqrt{-4x^2+16x-15}\)
b,\(\left(9x-2\right)\sqrt{3x-1}+\left(10-9x\right)\sqrt{3-3x}-4\sqrt{-9x^2+12x-3}=4\)
c, \(\left(6x-5\right)\sqrt{x+1}-\left(6x+2\right)\sqrt{x-1}+4\sqrt{x^2-1}=4x-3\)
1. Giải phương trình nghiệm nguyên
a) \(x^2+4x+2018^{10}\)
b) \(x^2+4x+\left(y-1\right)^2=21\)
c) \(x^2+3\left(y-1\right)^2=2021\)
d) \(\left(3x-1\right)^{2020}-18\left(y-2\right)^{2019}=2019^{2020}\)
2. Tìm x,y ∈ Z
a) \(x^2-y^2+6y=56\)
b) \(x^2-4x+9y^2-6y=11\)
\(1,\\ b,\Leftrightarrow\left(x^2+4x+4\right)+\left(y-1\right)^2=25\\ \Leftrightarrow\left(x+2\right)^2+\left(y-1\right)^2=25\)
Vậy pt vô nghiệm do 25 ko phải tổng 2 số chính phương
\(2,\\ a,\Leftrightarrow x^2-\left(y^2-6y+9\right)=47\\ \Leftrightarrow x^2-\left(y-3\right)^2=47\)
Mà 47 ko phải hiệu 2 số chính phương nên pt vô nghiệm
\(b,\Leftrightarrow\left(x-2\right)^2+\left(3y-1\right)^2=16\)
Mà 16 ko phải tổng 2 số chính phương nên pt vô nghiệm
Đúng 2
Bình luận (1)
1a. Đề lỗi
1b.
PT $\Leftrightarrow (x+2)^2+(y-1)^2=25$
$\Leftrightarrow (x+2)^2=25-(y-1)^2\leq 25$
$(x+2)^2$ là scp không vượt quá $25$ nên có thể nhận các giá trị $0,1,4,9,16,25$
Nếu $(x+2)^2=0\Rightarrow (y-1)^2=25$
$\Rightarrow (x,y)=(-2, 6), (-2, -4)$
Nếu $(x+2)^2=1\Rightarrow (y-1)^2=24$ không là scp (loại)
Nếu $(x+2)^2=4\Rightarrow (y-1)^2=21$ không là scp (loại)
Nếu $(x+2)^2=9\Rightarrow (y-1)^2=16$
$\Rightarrow (x,y)=(1, 5), (1, -3), (-5,5), (-5, -3)$
Nếu $(x+2)^2=25\Rightarrow (y-1)^2=0$
$\Rightarrow (x,y)=(3, 1), (-7, 1)$
Đúng 1
Bình luận (0)
1c.
Vì $x^2$ là scp nên $x^2\equiv 0,1\pmod 3$
$3(y-1)^2\equiv 0\pmod 3$
$\Rightarrow x^2+3(y-1)^2\equiv 0,1\pmod 3$
Mà $2021\equiv 2\pmod 3$
Do đó pt $x^2+3(y-1)^2=2021$ vô nghiệm
1d.
Ta thấy:
$(3x-1)^{2020}$ là scp không chia hết cho $3$ nên $(3x-1)^{2020}\equiv 1\pmod 3$
$18(y-2)^{2019}\equiv 0\pmod 3$
$\Rightarrow (3x-1)^{2020}+18(y-2)^{2019}\equiv 1\pmod 3$
Mà $2019^{2020}\equiv 0\pmod 3$
Do đó pt vô nghiệm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm x
1) 70 : \(\frac{4x+720}{x}\) = 1/2
2) \(\frac{3}{\left(x+2\right)\left(x+5\right)}+\frac{5}{\left(x+5\right)\left(x+10\right)}+\frac{7}{\left(x+10\right)\left(x+17\right)}=\frac{x}{\left(x+2\right)\left(x+17\right)}\) Với x không thuộc { -2; -5; -10; -17 }
\(1\)) \(70:\frac{4x+720}{x}=\frac{1}{2}\)
\(\Leftrightarrow\frac{4x+720}{x}=70:\frac{1}{2}\)
\(\Leftrightarrow\frac{4x+720}{x}=140\)
\(\Leftrightarrow\left(4x+720\right):x=140\)
\(\Leftrightarrow4x+720=140.x\)
\(\Leftrightarrow4x-140x=-720\)
\(\Leftrightarrow x.\left(-136\right)=-720\)
\(\Leftrightarrow x=-720:\left(-136\right)\)
\(\Leftrightarrow x=\frac{90}{17}\)
\(2\)) Mình đang nghĩ
Đúng 0
Bình luận (0)
giải các phương trình sau:
a) \(\left(x-1\right)^2+x^2-1=\left(x+1\right)\left(x+3\right)\)
b) \(\left(x^2-4x\right)^2+\left(x-2\right)^2=10\)
c) \(x^4-4x^2+5\left|x^2-2\right|=-8\)
a) Ta có: \(\left(x-1\right)^2+x^2-1=\left(x+1\right)\left(x+3\right)\)
\(\Leftrightarrow\left(x-1\right)^2+\left(x-1\right)\left(x+1\right)=\left(x+1\right)\left(x+3\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-1+x+1\right)=\left(x+1\right)\left(x+3\right)\)
\(\Leftrightarrow\left(x-1\right)\cdot2x-\left(x+1\right)\left(x+3\right)=0\)
\(\Leftrightarrow2x^2-2x-\left(x^2+4x+3\right)=0\)
\(\Leftrightarrow2x^2-2x-x^2-4x-3=0\)
\(\Leftrightarrow x^2-6x-3=0\)
\(\Leftrightarrow x^2-6x+9-12=0\)
\(\Leftrightarrow\left(x-3\right)^2-12=0\)
\(\Leftrightarrow\left(x-3\right)^2=12\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=\sqrt{12}\\x-3=-\sqrt{12}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{12}+3=3+2\sqrt{3}\\x=-\sqrt{12}+3=3-2\sqrt{3}\end{matrix}\right.\)
Vậy: \(x=3\pm2\sqrt{3}\)
Đúng 0
Bình luận (0)
Tìm x biết : (đề không sai)
1.-4xleft(x-7right)+4xleft(x^2-5right) 28x^2-13
2.left(4x^2-5xright)left(3x+2right)-7xleft(x-7right) left(-4+xright)left(-2x+3right)+12x^3+2x^2
3.left(-4x^2-3right)left(2x+5right)-left(8x-3right) left(-x^2+2right)-5x^2left(x-6right)-3x^2-4
4.left(x-7right)left(x+5right)-left(x-3right)left(x-2right) 15x^2left(x+1right)-left(3x^2-1right) left(5x^2-2right)-21x^2
5.left(x-3right)left(-x+10right)+left(x-8right)left(x+3right) left(5x^2-1right)left(x+3right)-5x^3-15x^2...
Đọc tiếp
Tìm x biết : (đề không sai)
1.\(-4x\left(x-7\right)+4x\left(x^2-5\right)\) \(=28x^2-13\)
2.\(\left(4x^2-5x\right)\left(3x+2\right)-7x\left(x-7\right)\)= \(\left(-4+x\right)\left(-2x+3\right)+12x^3+2x^2\)
3.\(\left(-4x^2-3\right)\left(2x+5\right)-\left(8x-3\right)\) \(\left(-x^2+2\right)=-5x^2\left(x-6\right)-3x^2-4\)
4.\(\left(x-7\right)\left(x+5\right)-\left(x-3\right)\left(x-2\right)\) \(=15x^2\left(x+1\right)-\left(3x^2-1\right)\) \(\left(5x^2-2\right)-21x^2\)
5.\(\left(x-3\right)\left(-x+10\right)+\left(x-8\right)\left(x+3\right)\) \(=\left(5x^2-1\right)\left(x+3\right)-5x^3-15x^2\)
6.\(\left(-2x^2+5\right)\left(-x+3\right)-x^2\left(2x-6\right)\) \(=\left(x-1\right)\left(x+1\right)-\left(x-2\right)\left(x+4\right)\)
giải pt :
a,\(\left(6x-5\right)\sqrt{x+1}-\left(6x+2\right)\sqrt{x-1}+4\sqrt{x^2-1}=4x-3\)
b, \(\left(9x-2\right)\sqrt{3x-1}+\left(10-9x\right)\sqrt{3-3x}-4\sqrt{-9x^2+12x-3}=4\)
c, \(\left(13-4x\right)\sqrt{2x-3}+\left(4x-3\right)\sqrt{5-2x}=2+8\sqrt{-4x^2+16x-15}\)
Bài 2 Xét dấu biểu thức sau
1 , fleft(xright)x^2-sqrt{3}x+frac{3}{4}
2 , fleft(xright)-x^2+3x-2
3 , fleft(xright)x^4-4x+1
4 , fleft(xright)frac{3x+7}{x^2-x-2}
5 , fleft(xright)frac{x+2}{3x+1}-frac{x-2}{2x-1}
6 , fleft(xright)frac{1}{x^2-5x+4}-frac{1}{x^2-7x+10}
7 , fleft(xright)left(x-1right)left(x-3right)-frac{18}{x^2-4x-4}
8 , fleft(xright)left(x^2-1right)left(x-2right)
9 , fleft(xright)left(x+3right)left(-4x^2+9x-2right)
10 , fleft(xright)frac{10-x}{5+x^2}-frac{1}{2}
Đọc tiếp
Bài 2 Xét dấu biểu thức sau
1 , \(f\left(x\right)=x^2-\sqrt{3}x+\frac{3}{4}\)
2 , \(f\left(x\right)=-x^2+3x-2\)
3 , \(f\left(x\right)=x^4-4x+1\)
4 , \(f\left(x\right)=\frac{3x+7}{x^2-x-2}\)
5 , \(f\left(x\right)=\frac{x+2}{3x+1}-\frac{x-2}{2x-1}\)
6 , \(f\left(x\right)=\frac{1}{x^2-5x+4}-\frac{1}{x^2-7x+10}\)
7 , \(f\left(x\right)=\left(x-1\right)\left(x-3\right)-\frac{18}{x^2-4x-4}\)
8 , \(f\left(x\right)=\left(x^2-1\right)\left(x-2\right)\)
9 , \(f\left(x\right)=\left(x+3\right)\left(-4x^2+9x-2\right)\)
10 , \(f\left(x\right)=\frac{10-x}{5+x^2}-\frac{1}{2}\)