Thứ tự các số từ lớn đến nhỏ.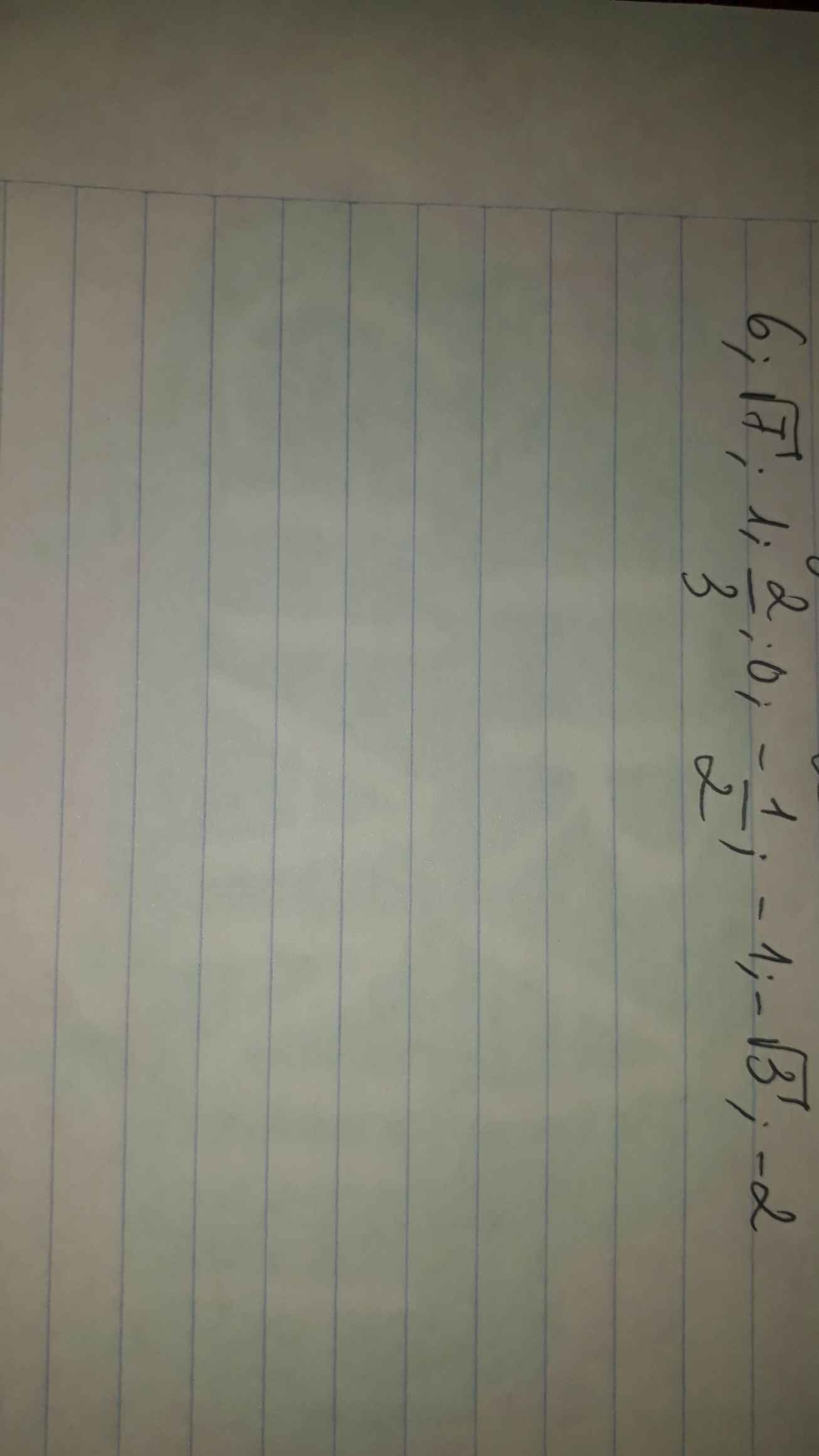

viết đoạn văn trình bày giải pháp để mình và mọi người tránh dịch covid

giúp với ạ

Bài 2 :

Giả sử \(a=\sqrt{3}\)là số hữu tỉ

Khi đó ta có \(a=\sqrt{3}=\frac{m}{n}\)với m, n tối giản ( n khác 0 )

Từ \(\sqrt{3}=\frac{m}{n}\Rightarrow m=\sqrt{3}n\)

Bình phương 2 vế ta được đẳng thức: \(m^2=3n^2\)(*)

\(\Rightarrow m^2⋮3\)mà m tối giản \(\Rightarrow m⋮3\)

=> m có dạng \(3k\)

Thay m vào (*) ta có : \(9k^2=3n^2\)

\(\Leftrightarrow3k^2=n^2\)

\(\Leftrightarrow n=\sqrt{3}k\)

Vì k là số nguyên => n không là số nguyên

=> điều giả sử là sai

=> \(\sqrt{3}\)là số vô tỉ

\(-2< -1,75< 0< \sqrt{5}< \pi< \dfrac{22}{7}< 5\dfrac{3}{6}.\)

-2<-1.75<0<_{√5<π<22/7<5 3/6}

\(\sqrt{16}=4;\dfrac{2}{3}=0,\left(6\right);\Omega=3,14;-\sqrt{5}\simeq-2,24\)

\(-5,6< -2,23< 0\)

=>\(-5,6< -\sqrt{5}< 0\)(1)

\(0< \dfrac{2}{3}< 3,14< 4\)

=>\(0< \dfrac{2}{3}< \Omega< \sqrt{16}\)(2)

Từ (1) và (2) suy ra \(-5,6< -\sqrt{5}< 0< \dfrac{2}{3}< \Omega< \sqrt{16}\)

\(\left| { - 3,2} \right| = 3,2;\,\,\,\,\,\left| {2,13} \right| = 2,13;\,\,\,\left| {\, - \sqrt 2 } \right| = \sqrt 2  = 1,41..;\,\,\,\,\left| { - \frac{3}{7}} \right| = \frac{3}{7} = 0,42...\)

Do \(0,42 < 1,41... < 2,13 < 3,2\) nên:

\(\left| { - \frac{3}{7}} \right| < \left| { - \sqrt 2 } \right| < \left| {2,13} \right| < \left| { - 3,2} \right|\).

Ta có:

\(-\frac{2}{3} = -0,\left( 6 \right);\,\,\,\,\,4,1;\,\,\, - \sqrt 2  =  - 1,414...;\,\,\,\,3,2;\\\pi  = 3,141...;\,\,\,\, - \frac{3}{4} =  - 0,75;\,\,\,\,\frac{7}{3} = 2,\left( 3 \right)\).

Do \( - 1,414... <  - 0,75 < -0,\left( 6 \right) < 2,\left( 3 \right) < 3,141... < 3,2 < 4,1\)

Nên \( - \sqrt 2  <  - \frac{3}{4} < -\frac{2}{3} < \frac{7}{3} < \pi  < 3,2 < 4,1.\)

Ta có: 

\(-\dfrac{2}{3}\approx-0,67;-\sqrt{2}\approx-1,41;-\dfrac{3}{4}=-0,75;\dfrac{7}{3}\approx2,33;\pi\approx3,14\)

Từ đó, ta có thứ tự sắp xếp: 

\(-\sqrt{2};-\dfrac{3}{4};-\dfrac{2}{3};1;2;\dfrac{7}{3};3;\pi;4\)

giúp mink với ik mink cần gấp lắm lun íiiiiiiiiii

a) 5, 1, 1/2, 0, -2/3, -2, -3

b) \(\sqrt{2}\), 1, 1/2, 0, -1, -4/3, \(-\sqrt{5}\), -3

a) \(1>\dfrac{1}{2}>0>-\dfrac{2}{3}>-1>-3\)

b) \(\sqrt{2}>1>\dfrac{1}{2}>0>-1>\dfrac{-4}{3}>-\sqrt{5}>-3\)