Một vật dao động điều hòa với phương trình x= 6cos(2πt-\(\dfrac{\pi}{3}\))cm. Tính độ dài quãng đường mà vật đi được trong khoảng thời gian t1=1,5s đến t2=\(\dfrac{13}{3}\)s.

Những câu hỏi liên quan
Một vật dao động điều hòa dọc theo trục Ox với phương trình: \(x=5cos\left(\pi t+\dfrac{2\pi}{3}\right)cm\). Quãng đường vật đi được từ thời điểm t1= 2(s)đến thời điểm t2= \(\dfrac{17}{3}\)(s) là bn?
Đối với những bài tìm quãng đường trong khoảng từ t1 đến t2 thì bạn lấy t2-t1 rồi phân tích chúng ra thành \(\left[{}\begin{matrix}t_2-t_1=n.\dfrac{T}{2}+t'\\t_2-t_1=n.T+t''\end{matrix}\right.\) để dễ dàng tính. Tuyệt đối ko được phân tích thành T/4 hay T/3; T/6;T/v.v. bởi nó ko luôn đúng trong các trường hợp, nếu bạn cần mình sẽ lấy ví dụ cụ thể. Giờ mình sẽ áp dụng vô bài của bạn
\(t_2-t_1=\dfrac{17}{3}-2=\dfrac{11}{3}\left(s\right)=3+\dfrac{2}{3}\)
\(T=\dfrac{2\pi}{\pi}=2s\Rightarrow t_2-t_1=3.\dfrac{T}{2}+\dfrac{2}{3}\)
Trong 3T/2 vật đi được quãng đường là: \(S_1=6A=30\left(cm\right)\)
Tại thời điểm t1=2s, lúc này vật đã quay được:\(\varphi=2\pi\left(rad\right)\) nghĩa là quay về vị trí ban đầu
Trong 2/3 s vật quay được góc: \(\varphi=\dfrac{2}{3}\pi\left(rad\right)\)
Sử dụng đường tròn lượng giác, vật ở vị trí có pha là 2pi/3, quay được góc 2pi/3 thì lúc này vật có li độ là: \(x=-2,5\left(cm\right)\)
Nghĩa là vật đi từ vị trí có li độ x1=-2,5 theo chiều âm đến vị trí có li độ x2=-2,5 theo chiều dương, vậy quãng đường vật đi được là: \(S_2=\dfrac{A}{2}+\dfrac{A}{2}=A=5\left(cm\right)\)
Vậy tổng quãng đường vật đi được là: \(S=S_1+S_2=35\left(cm\right)\)
Đúng 1
Bình luận (1)
Vật dao động điều hòa với phương trình x = 6cos(ωt – π/2) (cm). Sau thời gian t1 = 0,5s kể từ thời điểm ban đầu vật đi được quãng đường 3 cm. Sau khoảng thời gian t2 = 20,5s kể từ thời điểm ban đầu vật đi được quãng đường:
A. 123cm.
B. 75cm.
C. 72cm.
D. 81cm.
Chọn D
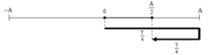
+ Lúc t = 0: xo = 0 và vo > 0 => để đi được s= 3 cm => đi đến x = 3 = A/2 => t1 = T/12 = 0,5 => T = 6 (s).
+ t2 = 20,5 (s) = 3T + 5T/12=> s = 3.4A + Δs (Δs là quãng đường đi thêm trong 5T/12).
+ Vì vật xuất phát ở xo = 0 và vo > 0 nên tách 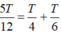 => Δs = A + A/2 = 1,5A.
=> Δs = A + A/2 = 1,5A.
+ Vậy, tổng quãng đường trong thời gian t2 là: s = 3/4A + 1,5A = 81 (cm).
Đúng 0
Bình luận (0)
Một vật dao động điều hòa theo trục Ox có phương trình li độ: x = 6cos (4πt -pi/3) (trong đó x tính bằng cm, t tính bằng s). Khoảng thời gian vật đi quãng đường 45 cm kể từ thời điểm t = 13s là
Ban đầu vật ở vị trí có pha ban đầu là -pi/3
Sau 13s, vật quét được góc: \(\varphi=\omega t=4\pi.13=52\pi\left(rad\right)\)
Vì góc quay được chia hết cho 2, nghĩa là sau 13s, vật sẽ quay về vị trí ban đầu có pha là -pi/3
\(\Rightarrow S=45cm=3+7.6=\dfrac{A}{2}+7A\)
Vậy vật quay được góc: \(\varphi=\dfrac{\pi}{3}+4\pi-\dfrac{\pi}{2}=\dfrac{23}{6}\pi\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{23\pi}{6.4\pi}=\dfrac{23}{24}\left(s\right)\)
Đúng 1
Bình luận (0)
(Câu 40 Đề thi THPT QG 2018 – Mã đề 210): Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm t1, vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t1 đến thời điểm t2 t1 +
1
6
(s), vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong khoảng thời gian từ thời điểm t2 đến thời điểm t3 t2 +
1
6
(s), vật đi được quãng đường 6 cm. Tốc độ cực đạ...
Đọc tiếp
(Câu 40 Đề thi THPT QG 2018 – Mã đề 210): Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm t1, vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t1 đến thời điểm t2 = t1 + 1 6 (s), vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong khoảng thời gian từ thời điểm t2 đến thời điểm t3 = t2 + 1 6 (s), vật đi được quãng đường 6 cm. Tốc độ cực đại của vật trong quá trình dao động là
A. 37,7 m/s
B. 0,38 m/s
C. 1,41 m/s
D. 224 m/s
Đáp án C
![]()
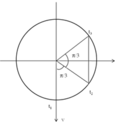
Thời gian đi từ t1 (x = 0) đến t2 ( v = 1 2 v m a x → x = ± A 3 2 ) là:
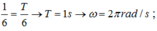
Thời gian đi từ t2 đến t3 là T/6 = (T/12 +T/12) nên tại t3 là vị trí x= ± A 3 2 nên ta có
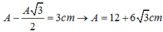
![]()
Đúng 0
Bình luận (0)
Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm
t
1
, vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t1 đến thời điểm
t
2
t
1
+
1
6
s
, vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong khoảng thời gian từ thời điểm
t...
Đọc tiếp
Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm t 1 , vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t1 đến thời điểm t 2 = t 1 + 1 6 s , vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong khoảng thời gian từ thời điểm t 2 đến thời điểm t 3 = t 2 + 1 6 s , vật đi được quãng đường 7,5 cm. Tốc độ cực đại của vật trong quá trình dao động là
A. 1,41 m/s.
B. 22,4 m/s.
C. 1,76 m/s.
D. 37,7 m/s.
Đáp án C
+ Khoảng thời gian từ t 1 đến t 2 thì vật đi từ vị trí v m a x đến vị trí v m a x 2 nên góc quét được là φ = π 3
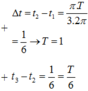
® Góc quét được từ t 2 đến t 3 là φ = π 3
+ Dựa vào đường tròn ta tìm được quãng đường vật đi từ t 2 đến t 3 là:
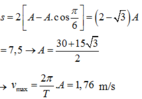
Đúng 0
Bình luận (0)
Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm
t
1
, vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm
t
1
đến thời điểm
t
2
t
1
+
1
6
(
s
)
, vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong...
Đọc tiếp
Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm t 1 , vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t 1 đến thời điểm t 2 = t 1 + 1 6 ( s ) , vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong khoảng thời gian từ thời điểm t 2 đến thời điểm t 3 = t 2 + 1 6 , vật đi được quãng đường 6cm. Tốc độ cực đại của vật trong quá trình dao động là
A. 1,41 m/s
B. 22,4 m/s
C. 0,38 m/s
D. 37,7 m/s
Chọn đáp án A
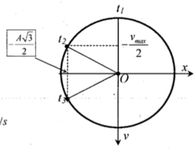
t 2 − t 1 = 1 6 s → v = v m a x 2 t 2 − t 1 = T 6 = 1 6 ⇒ T = 1 s t 2 − t 1 = 1 6 s = T 6 ⇒ S 23 = 2 A − A 3 2 = 6 c m → A = 22 , 4 c m ⇒ v m a x = A ω = 22 , 4 .2 π ≈ 140 c m / s = 1 , 4 m / s
Đúng 0
Bình luận (0)
Một vật dao động điều hoà với phương trình x8 cos(2πt+π/6)cm (t đo bằng giây). Quãng đường ngắn nhất mà vật đi được trong khoảng thời gian Δt4/3 s là A. 8 cm B.
20
3
cm
C. 40 cm D.
4
3
cm
Đọc tiếp
Một vật dao động điều hoà với phương trình x=8 cos(2πt+π/6)cm (t đo bằng giây). Quãng đường ngắn nhất mà vật đi được trong khoảng thời gian Δt=4/3 s là
A. 8 cm
B. 20 3 cm
C. 40 cm
D. 4 3 cm
Một vật dao động điều hoà theo phương trình x = 10cos(\(\pi t+\dfrac{\pi}{3}\)) cm. Thời gian tính từ lúc vật bắt đầu dao động động (t = 0) đến khi vật đi được quãng đường 30 cm là bao nhiêu
\(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\pi}=2\left(s\right)\)
Trong 1 nửa chu kì, vật di chuyển được quãng đường là \(2\cdot10=20\left(cm\right)\)
Vật khi đó phải đi từ vị trí có pha bằng \(-\dfrac{\pi}{3}\) đến vị trí có pha bằng \(\dfrac{\pi}{3}\), vì vật sẽ di chuyển được quãng đường \(\dfrac{A}{2}+\dfrac{A}{2}=A=10\left(cm\right)\)
Vậy thời gian vật phải đi là: \(\dfrac{T}{2}+\dfrac{T}{6}=\dfrac{2}{2}+\dfrac{2}{6}=\dfrac{4}{3}\left(s\right)\)
Đúng 2
Bình luận (0)
Một vật dao động điều hòa với phương trình:
x
4
2
cos
(
5
πt
-
3
π
4
)
cm
Quãng đường vật đi được từ thời điểm t1 1/10 (s) đến t2 6(s) là: A. 84,4cm B. 333,8cm C. 331,4cm D. 337,5cm
Đọc tiếp
Một vật dao động điều hòa với phương trình:
x = 4 2 cos ( 5 πt - 3 π 4 ) cm
Quãng đường vật đi được từ thời điểm t1 = 1/10 (s) đến t2 = 6(s) là:
A. 84,4cm
B. 333,8cm
C. 331,4cm
D. 337,5cm
Chọn C
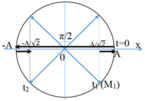
+ Chu kỳ: ![]()
+ Thời gian đi: t2 -t1 = 6- 1/10= 5,9 (s)
φ1 = 5πt1 - 3π/4 = -π/4
+ Ta có: 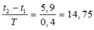
hay ![]()
+ Quãng đường đi được: S = 14.4A + ∆S
+Sau 14T kể từ thời điểm t1 vật trở lại vị trí cũ, và đi thêm 1 đoạn ∆S ứng với vật chuyển động tròn quay thêm góc ∆φ = 0,75.360o = 270o
+Quan sát hình vẽ ta tính được quãng đường đi trong 14T+ 0,75T là: S = 14.4A + 2A + 2.(A – A/ 2 ) = 331,4 cm
Đúng 0
Bình luận (1)










