Lời giải:

a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)

Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.

$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học

$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)

Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$

$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky

$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$

Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$

c. ĐKXĐ: $-2\leq x\leq 2$

$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky

$\Leftrightarrow y^2\leq 8$

$\Leftrightarrow y\leq 2\sqrt{2}$

Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$

Mặt khác:

$x\geq -2$

$\sqrt{4-x^2}\geq 0$

$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$

ĐKXĐ: \(1954\le x\le2014\)

y = \(\sqrt{x-1954}+\sqrt{2014-x}\ge\sqrt{x-1954+2014-x}=\sqrt{60}=2\sqrt{15}\)

ĐTXR <=> (x-1954)(2014-x) = 0  <=>\(\orbr{\begin{cases}x=1954\\x=2014\end{cases}}\)

Vậy GTNN y = \(2\sqrt{15}\)khi x = 1954 hoặc x = 2014

y = \(\sqrt{x-1954}+\sqrt{2014-x}\le\sqrt{2\left(x-1954+2014-x\right)}=\sqrt{2\cdot60}=\sqrt{120}=2\sqrt{30}\)

ĐTXR <=> x - 1954 = 2014 - x <=> x = 1984 (thỏa ĐKXĐ)

Vậy GTLN y = \(2\sqrt{30}\)khi x=1984

Bài này áp dụng bất đẳng thức phụ: \(\sqrt{a}+\sqrt{b}\ge\sqrt{a+b}\) (Dau "=" xay ra khi ab=0)

va bat dang thuc \(\sqrt{a}+\sqrt{b}\le\sqrt{2\left(a+b\right)}\) (Dau "=" xay ra khi a=b)

Ở dưới chưa chứng minh bất đẳng thức nên chứng minh thêm nha, không được ghi thẳng như ở dưới

ĐKXĐ : \(-1\le x\le3\)

- ADbu nhi : \(\left(\sqrt{x+1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(\left(\sqrt{x+1}\right)^2+\left(\sqrt{3-x}\right)^2\right)\)

\(=2\left(x+1+3-x\right)=2.4=8\)

\(\Rightarrow\sqrt{x+1}+\sqrt{3-x}\le\sqrt{8}=2\sqrt{2}\)

- Dấu " = " xảy ra \(\Leftrightarrow\dfrac{1}{\sqrt{x+1}}=\dfrac{1}{\sqrt{3-x}}\)

\(\Leftrightarrow x+1=3-x\)

\(\Leftrightarrow x=1\left(TM\right)\)

\(\Rightarrow Max_{f\left(x\right)}=2\sqrt{2}\) tại x = 1.

- Có : \(\sqrt{x+1}+\sqrt{3-x}\ge\sqrt{x+1+3-x}=\sqrt{4}=2\)

- Dấu " = " xảy ra <=> x = -1 ( TM )

\(\Rightarrow Min_{f\left(x\right)}=2\) tại x = - 1 .

a) Do \(-1\le sinx\le1,\forall x\in R\).
Nên giá trị lớn nhất của \(y=3-4sinx\) bằng \(3-4.\left(-1\right)=7\)khi \(sinx=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{2}+k\pi\).
Giá trị nhỏ nhất của \(y=3-4sinx\) bằng \(3-4.1=-1\) đạt được khi \(sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\).

b) \(y=2-\sqrt{cosx}\) xác định khi \(0\le cosx\le1\) .
Giá trị lớn nhất của \(y=2-\sqrt{cosx}=2-\sqrt{0}=2\) khi \(cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\).
Giá trị nhỏ nhất của \(y=2-\sqrt{cosx}=2-\sqrt{1}=1\) khi \(cosx=1\Leftrightarrow x=k2\pi\).

Đáp án C

Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .

Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3  trên R

* Bước 1: Tập xác định D = ℝ . Đạo hàm  y ' = 8 x 3 − 8 x   .

* Bước 2: Cho   y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .

* Bước 3: Ta có bảng biến thiên sau:

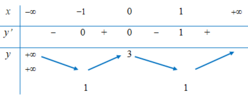
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.

Tham khảo:

Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} =  - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)

Hay \(S\left( { - 1;2} \right).\)

Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

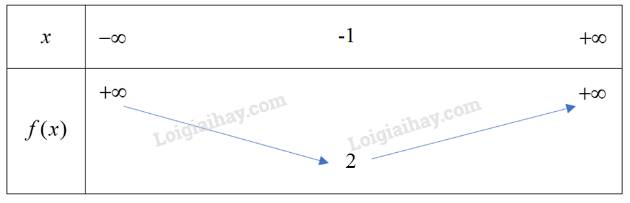
Hàm số đạt giá trị nhỏ nhất bằng \(2\).