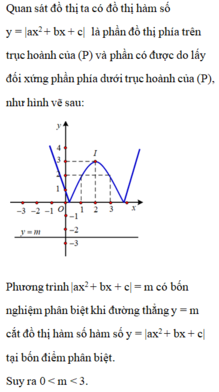
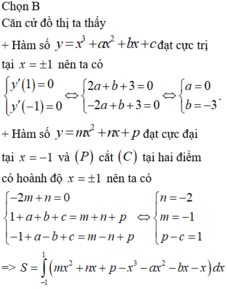Cho (P):y=ax2+bx+c có đồ thị như hình vẽ tìm a,b,c

Những câu hỏi liên quan
Cho hàm số
y
x
3
+
a
x
2
+
b
x
+
c
a
,
b
,
c
∈
ℝ
có đồ thị biểu diễn là đường cong (C) như hình vẽ. Khẳng định nào sau đây là sai? A.
a
+
b
+...
Đọc tiếp
Cho hàm số y = x 3 + a x 2 + b x + c a , b , c ∈ ℝ có đồ thị biểu diễn là đường cong (C) như hình vẽ. Khẳng định nào sau đây là sai?
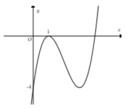
A. a + b + c = - 1
B. a 2 + b 2 + c 2 ≠ 132
C. a + c ≥ 2 b
D. a + b 2 + c 3 = 11
Cho hàm số
y
x
3
+
ax
2
+
bx
+
c
(
a
,
b
,
c
∈
ℝ
)
có đồ thị (C) và
y
mx
2
+
nx
+
p
(
m
,
n
,
p
∈
ℝ
)
có đồ thị (P)...
Đọc tiếp
Cho hàm số y = x 3 + ax 2 + bx + c ( a , b , c ∈ ℝ ) có đồ thị (C) và y = mx 2 + nx + p ( m , n , p ∈ ℝ ) có đồ thị (P) như hình vẽ. Tính diện tích hình phẳng giới hạn bởi (C) và (P) có giá trị nằm trong khoảng nào sau đây?
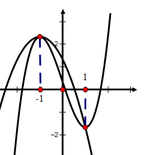
A. (0;1)
B. (1;2)
C. (2;3)
D. (3;4)
Cho hai hàm số
y
x
3
+
a
x
2
+
b
x
+
c
(
a
,
b
,
c
∈
ℝ
)
có đồ thị (C) và
y
m
x
2
+
n
x
+
p
(
m
,
m
,
p
∈...
Đọc tiếp
Cho hai hàm số y = x 3 + a x 2 + b x + c ( a , b , c ∈ ℝ ) có đồ thị (C) và y = m x 2 + n x + p ( m , m , p ∈ ℝ ) có đồ thị (P) như hình vẽ. Diện tích hình phẳng giới hạn bởi (C) và (P) có giá trị nằm trong khoảng nào sau đây?

A. 0 ; 1
B. 1 ; 2
C. 2 ; 3
D. 3 ; 4
Cho hai hàm số y
x
3
+
a
x
2
+
b
x
+
c
(
a
,
b
,
c
∈
R
)
có đồ thị (C) và y
m
x
2
+
n
x
+
p
(
m
,
n
,
p
∈
ℝ
)
có...
Đọc tiếp
Cho hai hàm số
y = x 3 + a x 2 + b x + c ( a , b , c ∈ R ) có đồ thị (C) và
y= = m x 2 + n x + p ( m , n , p ∈ ℝ ) có đồ thị (P) như hình vẽ. Diện tích hình phẳng giới hạn bởi (C) và (P) có giá trị nằm trong khoảng nào sau đây?
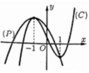
A. (0;1)
B. (1;2)
C. (2;3)
D. (3;4)
Phương pháp:
- Xét phương trình hoành độ giao điểm, tìm nghiệm.
- Diện tích hình phẳng giới hạn bởi các đồ thị hàm
y=f(x),y=g(x) và các đường thẳng
![]()
Cách giải:
Phương trình hoành độ giao điểm của (C) và (P) là
![]()
![]()
Dựa vào đồ thị ta thấy hai đồ thị hàm số tiếp
xúc nhau tại điểm có hoành độ x=-1 và cắt nhau
tại điểm có hoành độ x=1 nên phương trình (*)
có nghiệm x=-1 (bội 2) và x=1 (nghiệm đơn).
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Cho hàm số y ax2 + bx + c có đồ thị (P) như hình vẽ.Khẳng định nào sau đây là sai? A. Hàm số đồng biến trên khoảng (−
∞
; 3). B. (P) có đỉnh là I (3; 4). C. (P) cắt trục tung tại điểm có tung độ bằng 1. D. (P) cắt trục hoành tại hai điểm phân biệt.
Đọc tiếp
Cho hàm số y = ax2 + bx + c có đồ thị (P) như hình vẽ.

Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng (− ∞ ; 3).
B. (P) có đỉnh là I (3; 4).
C. (P) cắt trục tung tại điểm có tung độ bằng 1.
D. (P) cắt trục hoành tại hai điểm phân biệt.
Đáp án C
Đồ thị hàm số đi lên trên khoảng (− ∞ ; 3) nên đồng biến trên khoảng đó. Do đó A đúng.
Dựa vào đồ thị ta thấy (P) có đỉnh có tọa độ (3; 4). Do đó B đúng.
(P) cắt trục hoành tại hai điểm phân biệt có hoành độ −1 và 7. Do đó D đúng.
Dùng phương pháp loại trừ thì C là đáp án sai.
Đúng 0
Bình luận (0)
Cho hàm số
y
a
x
2
+
b
x
+
c
có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng? A. a0,b0,c0 B. a0,b0, c0 C. a0,b0,c0 D. a0,b0,c0
Đọc tiếp
Cho hàm số y = a x 2 + b x + c có đồ thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?

A. a>0,b=0,c>0
B. a>0,b>0, c>0
C. a>0,b<0,c>0
D. a<0,b>0,c>0
Cho parabol (P): y a
x
2
+ bx + c (a
≠
0) có đồ thị như hình bên. Tìm các giá trị m để phương trình |ax2 + bx + c| m có bốn nghiệm phân biệt. A. −1 m 3 B. 0 m 3. C. 0
≤
m
≤
3. D. −1
≤
m
≤
3.
Đọc tiếp
Cho parabol (P): y = a x 2 + bx + c (a ≠ 0) có đồ thị như hình bên. Tìm các giá trị m để phương trình |ax2 + bx + c| = m có bốn nghiệm phân biệt.
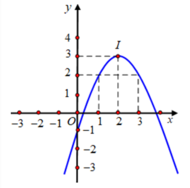
A. −1 < m < 3
B. 0 < m < 3.
C. 0 ≤ m ≤ 3.
D. −1 ≤ m ≤ 3.
Cho hai hàm số
y
x
3
+
a
x
2
+
b
x
+
c
a
,
b
,
c
∈
ℝ
có đồ thị (C) và
y
m
x
2
+
n
x
+
p...
Đọc tiếp
Cho hai hàm số y = x 3 + a x 2 + b x + c a , b , c ∈ ℝ có đồ thị (C) và y = m x 2 + n x + p m , n , p ∈ ℝ có đồ thị (P) như hình vẽ. Diện tích hình phẳng giới hạn bởi (C) và (P) có giá trị nằm trong khoảng nào sau đây?

A. (0;1)
B. (1;2)
C. (2;3)
D. (3;4)
Phương trình hoành độ giao điểm của (C) và (P) là
x 3 + a x 2 + b x + c = m x 2 + n x + p
⇔ x 3 + a - m x 2 + b - n x + c - p = 0 *
Dựa vào đồ thị ta thấy hai đồ thị hàm số tiếp xúc nhau tại điểm có hoành độ x=-1 và cắt nhau tại điểm có hoành độ x=1 nên phương trình (*) có nghiệm x=-1 (bội 2) và x=1 (nghiệm đơn).
Viết lại (*) ta được x + 1 2 x - 1 = 0
Vậy 

Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
liên tục trên đoạn
-
3
;
5
và có đồ thị như hình vẽ (phần cong của đồ thị là một phần của
P
:
y
a
x
2
+
b
x
+
c
). Tích phân
∫...
Đọc tiếp
Cho hàm số y = f x liên tục trên đoạn - 3 ; 5 và có đồ thị như hình vẽ (phần cong của đồ thị là một phần của P : y = a x 2 + b x + c ). Tích phân ∫ - 2 3 f x d x bằng

A. 53 2
B. 61 3
C. 95 7
D. 97 6
Cho parabol
(
P
)
:
y
a
x
2
+
b
x
+
c
, (a ≠ 0) có đồ thị như hình bên. Khi đó 2a + b + 2c có giá trị là: A. -9 B. 9 C. -6 D. 6
Đọc tiếp
Cho parabol ( P ) : y = a x 2 + b x + c , (a ≠ 0) có đồ thị như hình bên. Khi đó 2a + b + 2c có giá trị là:

A. -9
B. 9
C. -6
D. 6