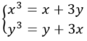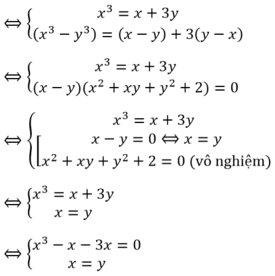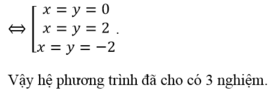\(P=x^3+y^3+2021xy\)

\(=\left(x+y\right)^3-3xy\left(x+y\right)+2021xy\)

\(=\left(\dfrac{2021}{3}\right)^3=\dfrac{8254655261}{27}\)

\(3x+3y=2021\)

\(\Leftrightarrow x+y=\dfrac{2021}{3}\)

\(P=x^3+y^3+2021xy\)

\(=\left(x+y\right)^3-3xy\cdot\left(x+y\right)+2021xy\)

\(=\left(\dfrac{2021}{3}\right)^3-3xy\cdot\dfrac{2021}{3}+2021xy\)

\(=\dfrac{8254655261}{27}\)

\(A=2x^2+y^2-2x+2xy+2y+3=y^2+2y\left(x+1\right)+\left(x+1\right)^2+\left(x^2-4x+4\right)-2=\left(y+x+1\right)^2+\left(x-2\right)^2-2\ge-2\)

\(minA=-2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)

\(P=x^3+2021xy+y^3\)

\(=\left(x+y\right)^3-3xy\left(x+y\right)+2021xy\)

\(=\left(\dfrac{2021}{3}\right)^3\)

\(=\dfrac{8254655261}{27}\)

Ta có: \(x^3-y^3=3x-3y\Leftrightarrow x^2+xy+y^2=3\) (Do \(x\neq y\)).

Tương tự: \(y^2+yz+z^2=3;z^2+zx+x^2=3\).

Cộng vế với vế ta có: \(2\left(x^2+y^2+z^2\right)+xy+yz+zx=9\)

\(\Leftrightarrow\dfrac{3\left(x^2+y^2+z^2\right)}{2}+\dfrac{\left(x+y+z\right)^2}{2}=9\).

Mặt khác, từ đó ta cũng có: \(\left(x^2+xy+y^2\right)-\left(y^2+yz+z^2\right)=0\Leftrightarrow\left(x+y+z\right)\left(x-z\right)=0\Leftrightarrow x+y+z=0\).

Do đó \(x^2+y^2+z^2=6\left(đpcm\right)\).

Cặc

Bài 5

a) A = -x³ + 6x² - 12x + 8

= -x³ + 3.(-x)².2 - 3.x.2² + 2³

= (-x + 2)³

= (2 - x)³

Thay x = -28 vào A ta được:

A = [2 - (-28)]³

= 30³

= 27000

b) B = 8x³ + 12x² + 6x + 1

= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³

= (2x + 1)³

Thay x = 1/2 vào B ta được:

B = (2.1/2 + 1)³

= 2³

= 8

Bài 6

a) 11³ - 1 = 11³ - 1³

= (11 - 1)(11² + 11.1 + 1²)

= 10.(121 + 11 + 1)

= 10.133

= 1330

b) Đặt B =  x³ - y³ = (x - y)(x² + xy + y²)

= (x - y)(x² - 2xy + y² + 3xy)

= (x - y)[(x - y)² + 3xy]

Thay x - y = 6 và xy = 9 vào B ta được:

B = 6.(6² + 3.9)

= 6.(36 + 27)

= 6.63

= 378

Bài 6 :

a) \(11^3-1=\left(11-1\right)\left(11^2+11+1^2\right)\)

\(\)\(=10.\left(121+12\right)\)

\(=10.133\)

\(=1330\)

b) \(\left\{{}\begin{matrix}x-y=6\\xy=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-2xy=36\\xy=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-2.18=36\\xy=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=72\\xy=9\end{matrix}\right.\)

Ta có :

\(x^3-y^3=\left(x-y\right)\left(x^2+y^2+xy\right)\)

\(=6.\left(72+9\right)\)

\(=6.81\)

\(=486\)

a) \(x^3-3x+3y-y^3=\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)=\left(x-y\right)\left(x^2+xy+y^2-3\right)\)

\(a,=\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)\\ =\left(x-y\right)\left(x^2+xy+y^2-3\right)\\ b,=\left(x+2\right)^2-\left(x-1\right)^2\\ =\left(x+2-x+1\right)\left(x+2+x-1\right)\\ =3\left(2x+1\right)\)

b) \(\left(x+2\right)^2-x^2+2x-1=\left(x+2\right)^2-\left(x^2-2x+1\right)=\left(x+2\right)^2-\left(x-1\right)^2=\left(x+2+x-1\right)\left(x+2-x+1\right)=3\cdot\left(2x+1\right)\)

a) (x - y)(x + y + 3).                    b) (x + y - 2xy)(2 + y + 2xy).

c) x 2 (x + l)( x 3  -  x 2  + 2).              d) (x – 1 - y)[ ( x   -   1 ) 2   +   ( x   -   1 ) y   +   y 2 ].

Đáp án: B

c) \(3x+3y-x^2-2xy-y^2=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)d) \(=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\)

\(=\left(x+y\right)\left(x+y+1\right)\left(x+y-1\right)\)

\(c,=3\left(x+y\right)-\left(x+y\right)^2=\left(3-x-y\right)\left(x+y\right)\\ d,=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)

c) \(=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)

d) \(\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]=\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)