a) Ví dụ:

\(\begin{array}{l}{x^2} - x + 1 > 0\\ - {x^2} + 5x + 5 \le 0\end{array}\)

b)

Bất phương trình bậc nhất: \(x - 1 > 0\)

Bất phương trình hai ẩn: \(2x + y < 5\)

- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.

- Bạn Phương nhận xét sai.

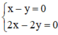Ví dụ: Xét hai hệ  và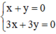 

Hệ 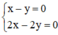 có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.

Hệ 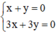 có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.

Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.

- Bạn Nga đã nhận xét đúng vì hai hệ phương trình cùng vô nghiệm có nghĩa là chúng cùng có tập nghiệm bằng ∅.

- Bạn Phương nhận xét sai.

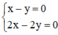Ví dụ: Xét hai hệ  và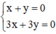 

Hệ 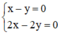 có vô số nghiệm. Tập nghiệm của (I) được biểu diễn bởi đường thẳng x – y = 0.

Hệ 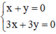 có vô số nghiệm. Tập nghiệm của (II) được biểu diễn bởi đường thẳng x + y = 0.

Nhận thấy, tập nghiệm của hai hệ (I) và hệ (II) được biểu diễn bởi hai đường thẳng khác nhau nên hai hệ không tương đương.

Kiến thức áp dụng

Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

- Phương châm về lượng là: Khi giao tiếp, cần nói cho có nội dung, nội dung của lời nói phải đáp ứng yêu cầu của cuộc giao tiếp, không thiếu, không thừa.

+ vd:  Bạn mua món này ở đâu đấy? -ngoài cửa hàng (vi phạm p/c về lượng)

- Phương châm về chất là: Khi giao tiếp, đừng nói những điều mà mình không tin là đúng hay không có bằng chứng xác thực.

+ vd: Tôi thấy một cái cây cao đến tận trời xanh. (Vi phạm p/c về chất)

Có 5 phương châm hội thoại chính gồm: Phương châm hội thoại về chất, phương châm về lượng, phương châm quan hệ, phương châm cách thức và phương châm lịch sự.

* Ví dụ 1: 

Người hàng xóm đến chơi mừng nhà mới của ông láng giềng. Nhìn lên mái nhà và nhìn quanh nhà, ông bảo: Nhà ta làm toàn bằng tre nứa loại tốt, nó mà cháy thì nổ to như đạn pháo

         Người nói vi phạm phương châm lịch sự, như có ý rủa nhà mới này sẽ cháy.

* Ví dụ 2 :

A hỏi B: Nhà cô giáo dạt Văn ở chỗ nào?

B đáp: Đâu như mạn bờ hồ Hoàn Kiếm

        B đã vi phạm phương châm về lượng ( câu trả lời không đúng yêu cầu của người hỏi)

...

HT

mình TL hơi thiếu nhưng mà mình chỉ biết đến đó thôi bạn ạ

sorry

a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)

Ví dụ: 2x + 4 = 0

a = 2; b = 4

b) Công thức tính thể tích hình hộp chữ nhật:

V = Sh

Với V là thể tích, S là diện tích 1 đáy, h là chiều cao

c)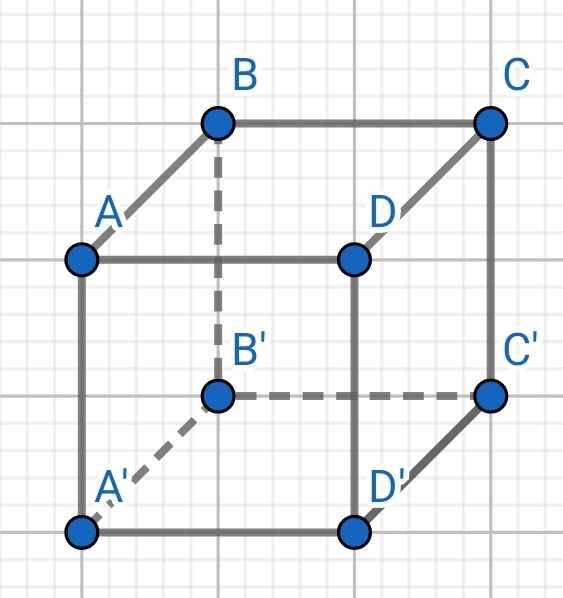   

Thể tích:

V = AB.AD.AA'

= 12 . 16 . 25 = 4800 (cm³)

a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn

b: V=a*b*c

a,b là chiều dài, chiều rộng

c là chiều cao

c: V=12*16*25=4800cm³

2x + 3 ≥ -6

Vế trái của bất phương trình: 2x + 3

Vế phải của bất phương trình: -6

Phương trình một ẩn: 2x + 4 = 0

Phương trình hai ẩn: 3x + 7y = 10

– Phương trình (a) có tập nghiệm là S1

Phương trình (b) có tập nghiệm là S2

Nếu S1 ⊂ S2 thì ta nói (b) là phương trình hệ quả của phương trình (a), kí hiệu: (a) ⇒ (b)

– Ví dụ : Phương trình x + 1 = 0 có tập nghiệm là S1 = {–1}

phương trình x2 – x – 2 = 0 có tập nghiệm là S2 = {–1; 2}

Ta có: S1 ⊂ S2 nên phương trình x2 – x – 2 = 0 là phương trình hệ quả của phương trình x + 1 = 0, kí hiệu:

x + 1 = 0 ⇒ x2 – x – 2 = 0.

Ví dụ: Hàm số y = x4 + 2x2 có y' = 4x3 + 4x

Phương trình y' = 0 chỉ có một nghiệm x = 0