cho x2+y2=1
tìm giá trị lớn nhất và nhỏ nhất của P=\(\frac{2\left(x^2+6xy\right)}{1+2xy+y^2}\)
cho x2+y2=1
tìm giá trị lớn nhất và nhỏ nhất của P=\(\frac{2\left(x^2+6xy\right)}{1+2xy+y^2}\)
cho 2 số thực x, y thay đổi thỏa mãn hệ thức \(x^2+y^2=1\). Tính giá trị lớn nhất của bieur thức P=\(\frac{2\left(x^2+6xy\right)}{1+2xy+2y^2}\)
\(P=\frac{2\left(x^2+6xy\right)}{1+2xy+2y^2}=\frac{2x^2+12xy}{x^2+2xy+3y^2}\left(x^2+y^2=1\right)\)
Xét \(y=0\Rightarrow x^2=1\Rightarrow x=\pm1\Rightarrow P=2\)Xét \(y\ne0\) chia cả tử và mẫu của P cho \(y^2\) có:\(P=\frac{2\left(\frac{x}{y}\right)^2+12\frac{x}{y}}{\left(\frac{x}{y}\right)^2+2\frac{x}{y}+3}\). Đặt \(t=\frac{x}{y}\Rightarrow P=\frac{2t^2+12t}{t^2+2t+3}\)
\(\Rightarrow\left(2-P\right)t^2+2\left(6-P\right)t-3P=0\)
Để pt trên có nghiệm thì:
\(\Delta'=\left(6-P\right)^2+3P\left(2-P\right)\ge0\)
\(\Leftrightarrow-2P^2-6P+36\ge0\Leftrightarrow-2\left(x-3\right)\left(x+6\right)\ge0\)
\(\Rightarrow-6\le P\le3\) (khuyến mãi luôn tìm Min, còn đề ko nhắc nên dấu "='' của Min tự tìm :v)
Đẳng thức xảy ra khi \(\left(x;y\right)=\left(\pm\frac{3}{\sqrt{10}};\pm\frac{1}{\sqrt{10}}\right)\) (của max nhé, min tự tìm)
Cho x, y>0 và x 2 + y 2 = 2 . Giá trị lớn nhất của biểu thức A = 2 x y bằng
A. 2
B. 1
C. 4
D. 3
Cho x, y >0 và x 2 + y 2 = 2 . Giá trị lớn nhất của biểu thức A = 2 x y bằng
A. 2
B. 1
C. 4
D. 3
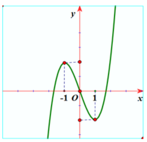
Cho x,y thỏa mãn 5 x 2 + 6 x y + 5 y 2 = 16 và hàm số bậc ba y = f(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của P = f x 2 + y 2 - 2 x 2 - y 2 - 2 x y + 4 . Tính M 2 + m 2
![]()
![]()
![]()
![]()
Cho 2 số thực x ; y thỏa mãn 0 < x ≤ 1 , 0 < y ≤ 1 và x + y = 3xy . Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x2 + y2 - 4xy
Tìm giá trị nhỏ nhất của các biểu thức sau
A=\(x^2-4x+1\) \(B=4x^2+4x+11\)
\(C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)\)
\(D=2x^2+y^2-2xy+2x-4y+9\)
Tìm giá trị lớn nhất của các biểu thức sau
\(E=5-8x-x^2\)
\(F=4x-x^2+1\)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của \(P=\frac{8x^2+6xy}{x^2+y^2}\)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của \(P=\frac{8x^2+6xy}{x^2+y^2}\).
Cả tử và mẫu đồng bậc:)) Em thử nha, ko chắc..
Với y = 0 thì x khác 0 và \(P=\frac{8x^2}{x^2}=8\)
Với y khác 0, chia cả tử và mẫu của P cho y2. Ta có:
\(P=\frac{8\left(\frac{x}{y}\right)^2+6.\frac{x}{y}}{\left(\frac{x}{y}\right)^2+1}\). Đặt \(\frac{x}{y}=t\).
Thế thì: \(P=\frac{8t^2+6t}{t^2+1}\)
Bí.
biểu thức đã cho (=) (8-P)x2 + 6yx -Py2=0
tìm denta ra thì đc như sau: y2(-P2+8P+9) >=0 =) -P2+8P+9 >=0
phần còn lại bấm máy tính ra kết quả là -1=<P=<9
Min=-1 và Max=9