\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)    

Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)

Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)

          \(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)

Bảng xét dấu:

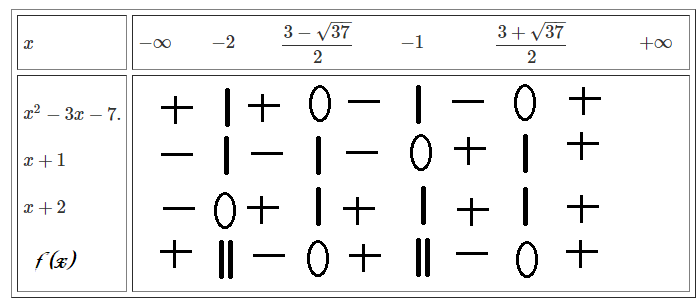
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)

\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)

Đặt \(f\left(x\right)=x^2-3x-7.\)

\(f\left(x\right)=x^2-3x-7.\)

\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)

a.\(A=\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}=\dfrac{\left(x-2\right)^2}{\left(x^2-4\right)\left(x-2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\)

\(A=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}\left(x\ne\pm2\right)\\ A=\dfrac{\left(x-2\right)^2}{\left(x-2\right)^2\left(x+2\right)}=\dfrac{1}{x+2}\\ B=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\left(x>0\right)\\ B=\dfrac{4\sqrt{x}\left(\sqrt{x}+1\right)}{3\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)

a) \(\dfrac{3x^2+1}{\sqrt{x-1}}=\dfrac{4}{\sqrt{x-1}}\)

ĐKXĐ: \(x>1\)

\(3x^2+1=4\)

\(3x^2=3\)

\(x^2=1\)

\(x=\pm1\)

=> Pt vô nghiệm

b) ĐKXĐ: x>-4

\(x^2+3x+4=x+4\)

\(x^2+2x=0\)

\(x\left(x+2\right)=0\)

\(\left[{}\begin{matrix}x=0\\x+2=0\Leftrightarrow x=-2\end{matrix}\right.\)

c) Đkxđ: \(3x-2>0\Leftrightarrow x>\dfrac{2}{3}\)
Pt \(\Leftrightarrow3x^2-x-2=3x-2\)
\(\Leftrightarrow3x^2-4x=0\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\left(l\right)\\x=\dfrac{4}{3}\left(tm\right)\end{matrix}\right.\)
Vậy \(x=\dfrac{4}{3}\) là nghiệm của phương trình.
d) Đkxđ: \(x\ne1\)
\(2x+3+\dfrac{4}{x-1}=\dfrac{x^2+3}{x-1}\) \(\Leftrightarrow\dfrac{\left(2x+3\right)\left(x-1\right)}{x-1}+\dfrac{4}{x-1}=\dfrac{x^2+3}{x-1}\)
\(\Leftrightarrow\left(2x+3\right)\left(x-1\right)+4=x^2+3\)
\(\Leftrightarrow x^2+x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(l\right)\\x=-2\left(tm\right)\end{matrix}\right.\)
Vậy \(x=-2\) là nghiệm của phương trình.

1: ĐKXĐ: -2/2x-2>=0

=>2x-2<0

=>x<1

2: ĐKXĐ: 2/3x-1>=0

=>3x-1>0

=>x>1/3

3: ĐKXĐ: 2x-2/(-2)>=0

=>2x-2<=0

=>x<=1

4: ĐKXĐ: (3x-2)/5>=0

=>3x-2>=0

=>x>=2/3

5: ĐKXĐ: (x-2)/(x+3)>=0

=>x>=2 hoặc x<-3

a) ĐKXĐ: \(3\le x\le10\)

b) ĐKXĐ: \(\left\{{}\begin{matrix}x>-4\\x\ne4\end{matrix}\right.\)

c) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x\ne4\end{matrix}\right.\)

d) ĐKXĐ: \(x\ge\dfrac{1}{2}\)

e) ĐKXĐ: \(x\in R\)

a: ĐKXĐ: x^2-2x<>0 và x^2-1>0

=>(x>1 và x<>2) hoặc x<-1

b: ĐKXĐ: x+1>0 và 5-3x>0

=>x>-1 và 3x<5

=>-1<x<5/3

c: DKXĐ: 5x+3>=0 và 3-x>0

=>x>=-3/5 và x<3

=>-3/5<=x<3

d: ĐKXĐ: 4-x^2>0 và 1+x>=0

=>x^2<4 và x>=-1

=>-2<x<2 và x>=-1

=>-1<=x<2

e: ĐKXĐ: 2-3x<>0 và 1-6x>0

=>x<>2/3 và x<1/6

=>x<1/6