cho tam giác ABC,trọng tâm G.Gọi M,N,P theo thứ tự là các điểm đối xứng của A,B,C qua tâm G
a) chứng minh tứ giác BPNC là hình bình hành
b)chứng minh các tam giác ABC,MNP bằng nhau
c)chứng minh tam giác ABC,MNP có cùng trọng tâm
Những câu hỏi liên quan
3 tháng 12 2021 lúc 9:17
Cho tam giác ABC, trọng tâm G. Gọi M, N, P theo thứ tự là các điểm đối xứng của A, B, C qua tâm G.
a) Chứng minh tứ giác BPNC là hình bình hành.
b) Chứng minh các tam giác ABC, MNP bằng nhau.
c) Chứng minh các tam giác ABC, MNP có cùng trọng tâm
em cần gấp ạ
a: Xét tứ giác BPNC có
G là trung điểm của BN
G là trung điểm của PC
Do đó: BPNC là hình bình hành
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\) , trọng tâm G. Gọi M, N, P theo thứ tự là các điểm đối xứng của A, B, C qua tâm G. C/minh:
a, Tứ giác BPNC là hình bình hành
b, \(\Delta ABC=\Delta MNP\)
c, \(\Delta ABC\) và \(\Delta MNP\) có chung trọng tâm
Cho tam giác có G là trọng tâm .Gọi M,N,P thứ tự là trung điểm của AC,AB,BC và D,E,F thứ tự là điểm đối xứng của G qua M,N,P .Chứng minh
a, Tứ giác AGBE ,BGCF là hình bình hành
b, BE//GF,DG=CF
c, BC=ED
d, tam giác DEF = tam giác ABC
Cho tam giác nhọn ABC có AB AC. Gọi AD, BE, CF là các đường cao và H là trực tâm của tam giác ABC. Vẽ hình bình hành BHCG, đường thẳng G song song với BC cắt AH tại M
a) Chứng minh tứ giác ABGC và tứ giác ABMG nội tiếp được trong đường tròn.
b) Chứng minh tam giác ABD và tam giác AGC đồng dạng.
c) Chứng minh H và M đối xứng với nhau qua BC.
d) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC và K là trung điểm của BC, AK cắt OH tại I. Chứng minh rằng I là trọng tâm của tam giác ABC.
Đọc tiếp
Cho tam giác nhọn ABC có AB < AC. Gọi AD, BE, CF là các đường cao và H là trực tâm của tam giác ABC. Vẽ hình bình hành BHCG, đường thẳng G song song với BC cắt AH tại M
a) Chứng minh tứ giác ABGC và tứ giác ABMG nội tiếp được trong đường tròn.
b) Chứng minh tam giác ABD và tam giác AGC đồng dạng.
c) Chứng minh H và M đối xứng với nhau qua BC.
d) Gọi O là tâm đường tròn ngoại tiếp tam giác ABC và K là trung điểm của BC, AK cắt OH tại I. Chứng minh rằng I là trọng tâm của tam giác ABC.
Ai giúp em với😢
Cho tam giác ABC có G là trọng tâm .Gọi M,N,P thứ tự là trung điểm của AC,AB,BC và D,E,F thứ tự là điểm đối xứng của G qua M,N,P .Chứng minh
a, Tứ giác AGBE ,BGCF là hình bình hành
b, BE//GF,DG=CF
c, BC=ED
d, tam giác DEF = tam giác ABC
VẼ HÌNH
Cho tam giác ABC có G là trọng tâm .Gọi M,N,P thứ tự là trung điểm của AC,AB,BC và D,E,F thứ tự là điểm đối xứng của G qua M,N,P .Chứng minh
a, Tứ giác AGBE ,BGCF là hình bình hành
b, BE//GF,DG=CF
c, BC=ED
d, tam giác DEF = tam giác ABC
VẼ HÌNH
Cho tam giác ABC vuông tại A(AB<AC).Gọi M,N,P lần lượt là trung điểm các cạnh AB,BC,AC.Lấy D đối xứng C qua M ,NP và DA cắt nhau tại Q
a, Chứng minh tứ giác ABCD là hình bình hành
b, Chứng minh tứ giác AMNP là hình chữ nhật
c,Chứng minh M là trọng tâm tam giác DNP
cho tam giác ABC .Vẽ các điểm A* đối xứng với A qua C ,B* đối xứng với B qua A ,C*đối xứng với C qua B ,Trung tuyến BD của tam giác ABC cắt trung tuyến B*D* của tam giác A*B*C* tại O
a/chứng minh ABD*D là hình bình hành
b/chứng minh O là trọng tâm chung của tam giác ABC và tam giác A*B*C
Cho hình vuông ABCD. Gọi E là điểm đối xứng của điểm A qua điểm D. a) Chứng minh tam giác ACE là tam giác vuông cân. b) Từ A hạ AH ^ BE, gọi M và N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác BMNC là hình bình hành. c) Chứng minh M là trực tâm của tam giác ANB. d) Chứng minh
A
N
C
^
90
0
.
Đọc tiếp
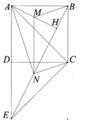
Cho hình vuông ABCD. Gọi E là điểm đối xứng của điểm A qua điểm D.
a) Chứng minh tam giác ACE là tam giác vuông cân.
b) Từ A hạ AH ^ BE, gọi M và N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác BMNC là hình bình hành.
c) Chứng minh M là trực tâm của tam giác ANB.
d) Chứng minh A N C ^ = 90 0 .
a) E là điểm đối xứng của điểm A qua điểm D Þ A, D, E thẳng hàng và DA = DE Þ CD ^ AE tại trung điểm của AE Þ CA = CE Þ DCAE cân ở C.
Þ D A C ^ = 450 Þ DACE vuông cân.
b) Áp dụng tính chất đường trung bình cho DHAE và giả thiết ABCD là hình vuông ta sẽ chứng minh được tứ giác BMNC là hình bình hành.
c) Do AH ^ BN, mà NM//CB Þ NM ^ AB nên M là trực tâm của tam giác ANB.
d) M là trực tâm DABN nên BM ^ AN mà BM//CN Þ A N C ^ = 900
Đúng 0
Bình luận (0)