Chứng minh rằng I là trung điểm của AB \(⇌\)\(\overrightarrow{IA}+\overrightarrow{IB}=0\)

Những câu hỏi liên quan
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng overrightarrow{MI}overrightarrow{IN}b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết overrightarrow{IA}+overrightarrow{IB}+overrightarrow{IC}+overrightarrow{ID}overrightarrow{0}. Chứng minh rằng tứ giác ABCD là hình bình hành
Đọc tiếp
a) Cho tứ giác ABCD không phải là hình bình hành, AC cắt BD tại O có OB = OD. Gọi M, N lần lượt là trung điểm của AB và CD, MN cắt AC tại I. Chứng minh rằng \(\overrightarrow{MI}=\overrightarrow{IN}\)
b) Cho tứ giác ABCD có 2 đường chéo cắt nhau tại I. Biết \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\). Chứng minh rằng tứ giác ABCD là hình bình hành
cho đoạn thẳng AB và I nằm giữa AB
a) chứng minh rằng\(IB.\overrightarrow{IA}+IA.\overrightarrow{IB}=0\)
Giả sử \(\frac{IA}{AB}=k\Rightarrow\frac{IB}{AB}=1-k\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=-k\overrightarrow{AB}\\\overrightarrow{IB}=\left(1-k\right)\overrightarrow{AB}\end{matrix}\right.\)
\(\Rightarrow IB.\overrightarrow{IA}+IA.\overrightarrow{IB}=\left(1-k\right).AB.\left(-k\right)\overrightarrow{AB}+k.AB.\left(1-k\right)\overrightarrow{AB}\)
\(=\left(k^2-k\right)AB.\overrightarrow{AB}+\left(k-k^2\right)AB.\overrightarrow{AB}\)
\(=\left(k^2-k+k-k^2\right).AB.\overrightarrow{AB}=\overrightarrow{0}\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD . Gọi E, F lần lượt là trung điểm của AB và CD, I là trung điểm của EF:
a/ Chứng minh : \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
b/ Chứng minh : \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=\overrightarrow{4MI}\) , với M tùy ý
Cho hai điểm phân biệt A và B. Điều kiện để điểm I là trung điểm của đoạn thẳng AB là :
a) IA = IB
b) \(\overrightarrow{IA}=\overrightarrow{IB}\)
c) \(\overrightarrow{IA}=-\overrightarrow{IB}\)
d) \(\overrightarrow{AI}=\overrightarrow{BI}\)
Câu C: \(\overrightarrow{IA}=-\overrightarrow{IB}\)
Đúng 0
Bình luận (0)
đường tròn nội tiếp (I) của tam giác ABC theo thứ tự tiếp xúc với các cạnh BC,CA,AB tại D,E,F. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\)
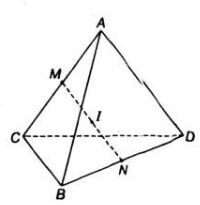
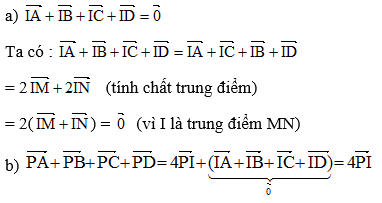
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh :
a) overrightarrow{IA}+overrightarrow{IB}+overrightarrow{IC}+overrightarrow{ID}overrightarrow{0}
b) overrightarrow{PI}dfrac{1}{4}left(overrightarrow{PA}+overrightarrow{PB}+overrightarrow{PC}+overrightarrow{PD}right)
Đọc tiếp
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh :
a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
b) \(\overrightarrow{PI}=\dfrac{1}{4}\left(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}\right)\)
Cho \(\Delta ABC\), gọi I là trung điểm của cạnh AC. Tìm điểm M thỏa mãn điều kiện: \(\overrightarrow{IB}+\overrightarrow{IA}-\overrightarrow{IC}-\overrightarrow{CM}=\overrightarrow{0}\)
Can u help me???
please, luv u (tymtymtym)
→IB+→IA−→IC−→CM=→0
=>\(\overrightarrow{IB}+\overrightarrow{IA}-\overrightarrow{IM}=\overrightarrow{0}\)
=>\(\overrightarrow{IB}+\overrightarrow{IA}=\overrightarrow{IM}\)
Đặt K là trung điểm AB
=>\(\overrightarrow{IB}+\overrightarrow{IA}=\overrightarrow{2IK}\)(T/c trung tuyến)
=>\(\overrightarrow{2IK}=\overrightarrow{IM}\)
=>K,M,I thẳng hàng
Vậy điểm M thuộc đoạn KI sao cho \(\dfrac{\overrightarrow{IK}}{\overrightarrow{IM}}=\dfrac{1}{2}\)
Đúng 3
Bình luận (1)
đường tròn nội tiếp (I) của tam giác ABC theo thứ tự tiếp xúc với các cạnh BC,CA,AB tại D,E,F. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\)
Cho tam giác ABC vông tại A, I là trung điểm của đường cao AH. CMR: \(BC^2.\overrightarrow{IA}+AC^2.\overrightarrow{IB}+AB^2.\overrightarrow{IC}=\overrightarrow{0}\).
Lời giải:
Áp dụng các công thức sau: \(|\overrightarrow {a}|^2=\overrightarrow{a}.\overrightarrow{a}\)
\(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{0}\) nếu \(\overrightarrow{a}\perp \overrightarrow{b}\)
Ta có:
\(BC^2.\overrightarrow{IA}+AC^2.\overrightarrow{IB}+AB^2.\overrightarrow{IC}\)
\(=BC^2.\overrightarrow{IA}+AC^2.(\overrightarrow{IA}+\overrightarrow{AB})+AB^2.(\overrightarrow{IA}+\overrightarrow{AC})\)
\(=BC^2.\overrightarrow{IA}+\overrightarrow{IA}(AC^2+AB^2)+AC^2.\overrightarrow{AB}+AB^2.\overrightarrow{AC}\)
\(=2BC^2.\overrightarrow{IA}+AC^2.\overrightarrow{AB}+AB^2.\overrightarrow{AC}\)
\(=\overrightarrow{BC}.\overrightarrow{BC}.\overrightarrow{HA}+\overrightarrow{AC}.\overrightarrow{AC}.\overrightarrow{AB}+\overrightarrow{AB}.\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\overrightarrow {BC}.\overrightarrow{0}+\overrightarrow{AC}.\overrightarrow{0}+\overrightarrow{AB}.\overrightarrow{0}=\overrightarrow {0}\)
Đúng 0
Bình luận (2)