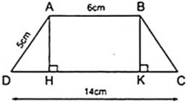
Kẻ AH ⊥ CD, BK ⊥ CD thì AH//BK nên hình thang ABKH có hai cạnh bên song song.

Áp dụng tính chất của hình thang ABKH có hai cạnh bên song song, ta có: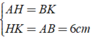

Áp dụng định lí Py – ta – go vào tam giác ADH vuông tại H ta được:

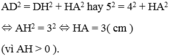
Vậy chiều cao của hình thang cân là 3cm.

a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)

b) Xem hình vẽ

Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)

Vì ABCD là hình thang cân nên AE = FB = 3.

Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.

\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)

1. Tính được AH=3cm theo định lý Pitago, vẽ đường cao CK (K thuộc AB), tính được BK=3cm nên HK=6cm nên AB=12cm, lúc đó sẽ tinhd được diện tích hình thang

2. Tương tự

Chu vi hình thang cân là:

3+5+4+4=16(cm)

              Đ/S:...

Vì ABCD là hình thang cân

=> AD = BC = 4cm

Chu vi hình thang cân ABCD là : 3+4+5+4=16 (cm)

Giải

Chu vi hình thang cân là :

3 + 5 + 4 + 4 = 16 ( cm )

Đáp số : 16 cm

AB=CD-6=16-6=10(cm)

\(AD=\dfrac{AB}{2}=5\left(cm\right)\)

Vì ABCD là hình thang cân

nên \(AD=BC=5\left(cm\right)\)

Chu vi hình thang cân ABCD là:

\(AB+AD+CD+BC=5+5+10+16=36\left(cm\right)\)

Diện tích hình thang cân ABCD là:

\(S_{ABCD}=\dfrac{1}{2}\cdot AH\cdot\left(AB+CD\right)\)

\(=\dfrac{1}{2}\cdot4\cdot\left(10+16\right)=2\cdot26=52\left(cm^2\right)\)

Cạnh AB dài:

16 - 6 = 10 (cm)

Cạnh AD dài:

10 : 2 = 5 (cm)

Chu vi hình thang cân ABCD:

16 + 10 + 5 + 5 = 36 (cm)

Diện tích hình thang:

(16 + 10) × 4 : 2 = 52 (cm²)

Cho hình thang cân ABCD có chu vi bằng 56cm, độ dài cạnh bên AB=5cm, chiều cao =4cm. Tính diện tích hình thang cân đó

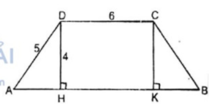
Xét hình thang cân ABCD có AB // CD

Đáy nhỏ CD = 6cm, cạnh bên AD = 5cm

Đường cao DH = 4cm. Kẻ CK ⊥ AB

Ta có tứ giác CDHK là hình chữ nhật

HK = CD = 6cm

△ AHD vuông tại H. Theo định lý Pi-ta-go ta có: A D 2 = A H 2 + D H 2

⇒  A H 2 = A D 2 - D H 2 = 5 2 - 4 2  = 25 – 16 = 9 ⇒ AH = 3cm

Xét hai tam giác vuông DHA và CKB :

∠ (DHA)= ∠ (CKB)= 90 0

AD = BC (tính chất hình thang cân)

∠ A =  ∠ B(gt)

Do đó:  △ DHA =  △ CKB (cạnh huyền, góc nhọn)

⇒ KB = AH = 3 (cm)

AB = AH + HK + KB = 3 + 6 + 3 = 12 (cm)

S A B C D  = (AB + CD) / 2. DH = (12 + 6) / 2. 4 = 36( c m 2 )

Áp dg cg thức tíh hìh thg là ra.

ko đc đâu pn ko áp dụng đc