khó was 

Mình quên không nói là đề bài yêu cầu chứng minh 2 bổ đề trên.

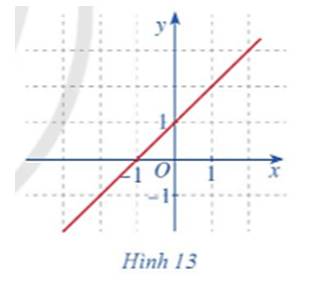
a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)

\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)

b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)

Ta c/m bđt

với \(x,y,z\ge1\) thì: \(\frac{x+y}{1+z}+\frac{y+z}{1+x}+\frac{z+x}{1+y}\ge\frac{6\sqrt[3]{xyz}}{1+\sqrt[3]{xyz}}\) (*)

dấu bằng xảy ra khi x=y=z

bđt (*) \(\Leftrightarrow\left(\frac{x+y}{1+z}+1\right)+\left(\frac{y+z}{1+x}+1\right)+\left(\frac{z+x}{1+y}+1\right)\ge\frac{6\sqrt[3]{xyz}}{1+\sqrt[3]{xyz}}+3\)

\(\Leftrightarrow\left(x+y+z+1\right)\left(\frac{1}{1+z}+\frac{1}{1+x}+\frac{1}{1+y}\right)\ge\frac{3+9\sqrt[3]{xyz}}{1+\sqrt[3]{xyz}}\)

Ta có: \(1+x+y+z\ge1+3\sqrt[3]{xyz}\)(1)

Với \(x,y\ge1\) ta chứng minh \(\frac{1}{1+x}+\frac{1}{1+y}\ge\frac{2}{1+\sqrt{xy}}\)(2)

\(\Leftrightarrow\frac{2+\left(x+y\right)}{1+\left(x+y\right)+xy}\ge\frac{2}{1+\sqrt{xy}}\Leftrightarrow2+\left(x+y\right)+2\sqrt{xy}+\sqrt{xy}\left(x+y\right)\ge2+2\left(x+y\right)+2xy\)

\(\Leftrightarrow2\sqrt{xy}\left(1-\sqrt{xy}\right)+\left(x+y\right)\left(\sqrt{xy}-1\right)\ge0\Leftrightarrow\left(\sqrt{x}-\sqrt{y}\right)^2\left(\sqrt{xy}-1\right)\ge0\)

bđt trên luôn đúng =>DPCM

đợi mình làm vế sau nữa nhé tại máy lag nên làm đk đến đây thôi xíu nữa hoặc mai mik làm vế sau cho nhé

Với \(x,y,z\ge1\) ta chứng minh: \(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge\frac{3}{1+\sqrt[3]{xyz}}\) (3)

\(\Leftrightarrow P=\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}+\frac{1}{1+\sqrt[3]{xyz}}\ge\frac{4}{1+\sqrt[3]{xyz}}\)

Áp dụng kết quả (2) ta thu được:

\(P\ge\frac{2}{1+\sqrt{xy}}+\frac{2}{1+\sqrt{z\sqrt[3]{xyz}}}\ge\frac{4}{1+\sqrt[4]{xyz\sqrt[3]{xyz}}}=\frac{4}{1+\sqrt[3]{xyz}}\)

Từ (1) và (3) suy ra (*) đúng

Trở lại bài toán: ta được bđt đã cho tưởng đương với:

\(\frac{\frac{1}{b}+\frac{1}{c}}{1+\frac{1}{a}}+\frac{\frac{1}{c}+\frac{1}{a}}{1+\frac{1}{b}}+\frac{\frac{1}{a}+\frac{1}{b}}{1+\frac{1}{c}}\ge\frac{\frac{6}{\sqrt[3]{abc}}}{1+\frac{1}{\sqrt[3]{abc}}}\)

Do x,y,z\(\le1\Rightarrow\frac{1}{x},\frac{1}{y},\frac{1}{z}\ge1\). Áp dụng (*) suy ra điều phải chứng minh dấu bằng xảy ra khi a=b=c

1.

Đặt \(\left(x;y;z\right)=\left(\dfrac{a}{a+b};\dfrac{b}{b+c};\dfrac{c}{c+a}\right)\Rightarrow\left\{{}\begin{matrix}1-x=\dfrac{b}{b+a}\\1-y=\dfrac{c}{b+c}\\1-z=\dfrac{a}{a+c}\end{matrix}\right.\)

\(\Rightarrow xyz=\dfrac{1}{8}\\ xyz=\left(1-x\right)\left(1-y\right)\left(1-z\right)\\ \Rightarrow xyz=1-\left(x+y+z\right)+\left(xy+yz+zx\right)-xyz\\ \Rightarrow2xyz=1-\left(x+y+z\right)+\left(xy+yz+zx\right)=\dfrac{1}{4}\\ \Rightarrow x+y+z=\dfrac{3}{4}+xy+yz+zx\)

\(\RightarrowĐpcm\)

2.