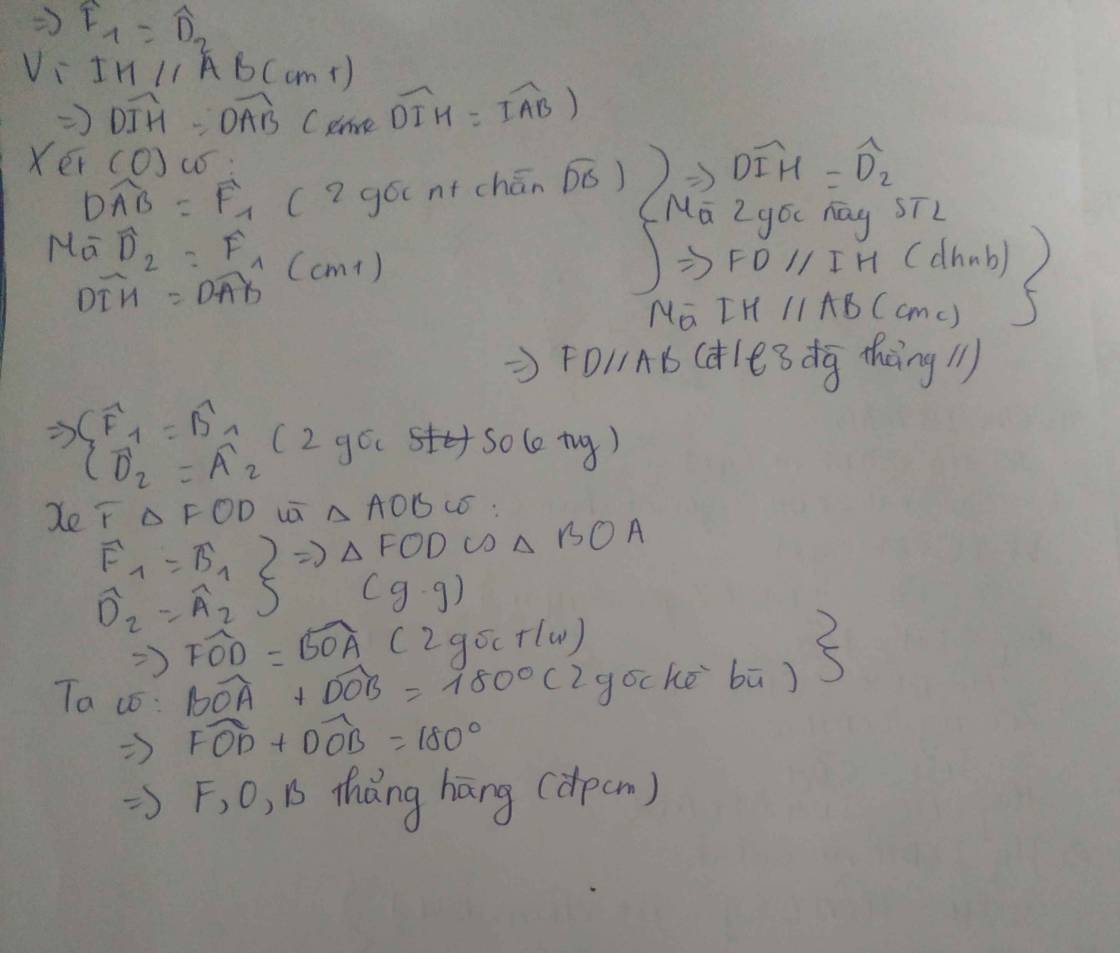Cho tam giác ABC (AB>AC) nội tiếp nửa đường tròn đường kính AB.Gọi H là chân đường vuông góc kẻ từ A đến tiếp tuyến với đường tròn tại C.AH cắt đường tròn tại M.Đường vuông góc với AC kẻ từ M cắt AC tại K và AB tại P
a> Cm MKCH nội tiếp
b> AC là phân giác của MAB
c> Tìm điều kiện tam giác ABC để M K O thảng hàng
Nhờ làm câu c ạ :v

Những câu hỏi liên quan
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là t...
Đọc tiếp
1. cho tam giác ABC.Tia Ax nằm khác phía với AC đối với đường thẳng AB thỏa mãn góc xAB bằng góc ACB.chứng minh Ax là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC
2.cho nửa đường tròn (O) đường kính AB trên đoạn AB lấy điểm M,gọi H là trung điểm của AM.đường thẳng qua H vuông góc với AB cắt (O) tại C .đường tròn đường kính MB cắt BC tại I. CM HI là tiếp tuyến của đường tròn đường kính MB
3.cho nửa đường tròn tâm O đường kính AB, C thuộc nửa đường tròn.vẽ CH vuông góc với AB(H thuộc AB),M là trung điểm CH,BM cắt tiếp tuyến Ax của O tại P .chứng minh PC là tiếp tuyến của (O)
4.cho đường tròn O đường kính AB, M là một điểm trên OB.đường thẳng qua M vuông góc với AB tại M cắt O tại C và D. AC cắt BD tại P,AD cắt BC tại Q,AB cắt PQ tai I chứng minh IC,ID là tiếp tuyến của (O)
5.cho tam giác ABC nội tiếp đường tròn đường kính BC (AB<AC).T là một điểm thuộc OC.đường thẳng qua T vuông góc với BC cắt AC tại H và cắt tiếp tuyến tại A của O tại P.BH cắt (O) tại D. chứng minh PD là tiếp tuyến của O
6.cho tam giác ABC nội tiếp đường tròn O. phân giác góc BAC cắt BC tại D và cắt (O) tại M chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H. AO cắt BC tại M. P, Q lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Chứng minh:
a/ H là tâm đường tròn nội tiếp tam giác DEF
b/ HE.MQ= HF. MP
c/ \(\dfrac{MB}{MC}.\dfrac{DB}{DC}=\left(\dfrac{AB}{AC}\right)^2\)
cho nửa đường tròn (0) đường kính AB, vẽ bán kình CO vuông góc với AB . M là 1 điểm bất kì trên cung AC .BM cắt AC tại H, gọi K là chân đường vuông góc kẻ từ H đến AB a) chứng minh tứ giác BCHK nội tiếp c) kẻ CP vuông góc với BM. trên đoạn BM lấy điểm E sao cho BE=AM chứng minh CM*MP= Pe
a) Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ACB}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{HCB}=90^0\)
Xét tứ giác HKBC có
\(\widehat{HKB}\) và \(\widehat{HCB}\) là hai góc đối
\(\widehat{HKB}+\widehat{HCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: HKBC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho tam giác ABC có: góc B = 90 độ + góc C , nội tiếp đường tròn O. Qua B kẻ đường thẳng vuông góc với BC cắt đường tròn O tại I, tiếp tuyến của đường tròn O kẻ từ A cắt BC tại H. Chứng minh :
a) AH vuông góc BC
b) AB^2 + AC^2 = 4R^2
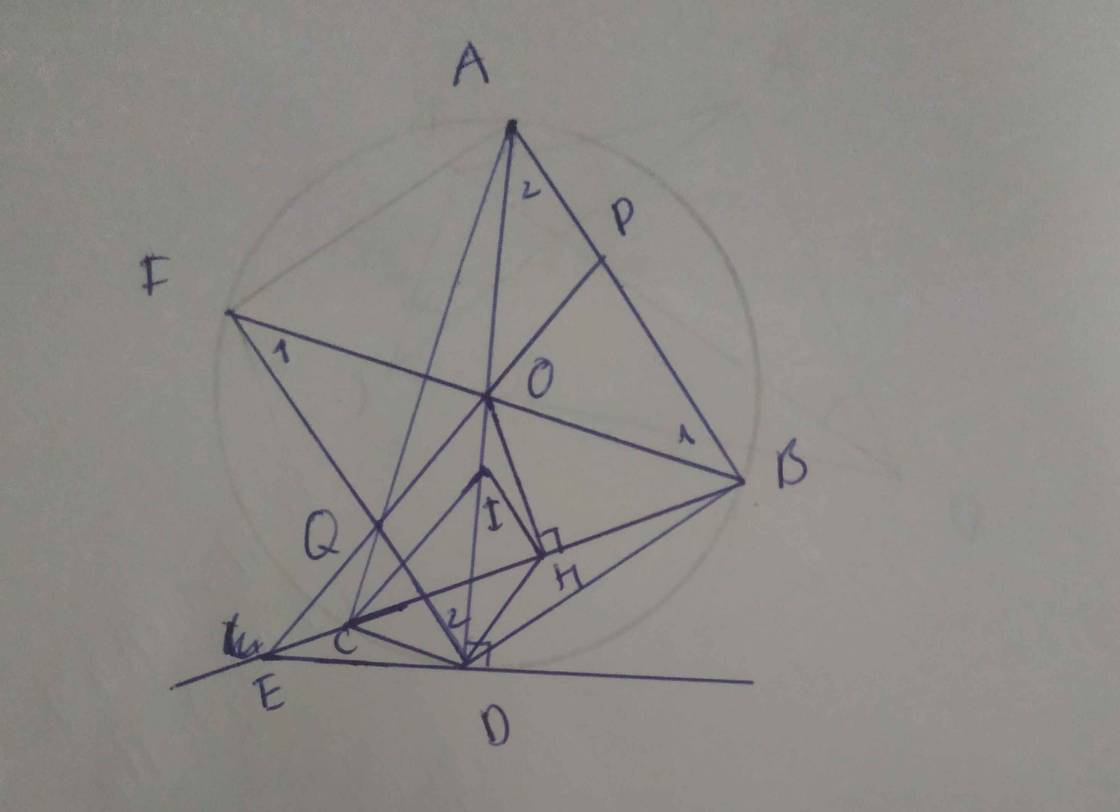
Cho đường tròn (O;R) ngoại tiếp tam giác nhọn ABC (ACAB). Kẻ đường kính AD của đường tròn (O). Tiếp tuyến tại D của đường tròn (O;R) cắt đường thẳng BC tại E. Kẻ OH vuông góc với BC tại H. Có OHDE nội tiếp. Có ED^2EC.EB. Từ C kẻ đường thẳng song song với OE, đường này cắt AD tại I. a) Chứng minh HI//ABb) Đường thẳng OE cắt AB và AC lần lượt tại P và Q. Gọi F là giao điểm thứ hai của DQ với đường tròn (O;R). Chứng minh ba điểm B,O,F thẳng hàng.
Đọc tiếp
Cho đường tròn (O;R) ngoại tiếp tam giác nhọn ABC (AC>AB). Kẻ đường kính AD của đường tròn (O). Tiếp tuyến tại D của đường tròn (O;R) cắt đường thẳng BC tại E. Kẻ OH vuông góc với BC tại H.
Có OHDE nội tiếp. Có ED^2=EC.EB.
Từ C kẻ đường thẳng song song với OE, đường này cắt AD tại I.
a) Chứng minh HI//AB
b) Đường thẳng OE cắt AB và AC lần lượt tại P và Q. Gọi F là giao điểm thứ hai của DQ với đường tròn (O;R). Chứng minh ba điểm B,O,F thẳng hàng.
cho tam giác ABC có 3 góc nhọn ( AB AC ) và nội tiếp đường tròn ( O ). Vẽ đường cao AH, ( H thuộc BC ) , từ H kẻ HM vuông góc với AB ( M thuộc AB ) và kẻ HN vuông góc với AC ( N thuộc AC ). Vẽ đường kính AE của đường tròn ( O ) cắt MN tại I. Tia MN cắt ( O) tại K. chứng minh rằnga, AMHN nội tiếp b, Delta AMNsimDelta ACBc, CEIN nội tiếp và tam giác AHK cân
Đọc tiếp
cho tam giác ABC có 3 góc nhọn ( AB < AC ) và nội tiếp đường tròn ( O ). Vẽ đường cao AH, ( H thuộc BC ) , từ H kẻ HM vuông góc với AB ( M thuộc AB ) và kẻ HN vuông góc với AC ( N thuộc AC ). Vẽ đường kính AE của đường tròn ( O ) cắt MN tại I. Tia MN cắt ( O) tại K. chứng minh rằng
a, AMHN nội tiếp
b, \(\Delta AMN\sim\Delta ACB\)
c, CEIN nội tiếp và tam giác AHK cân
a, Ta có: $HM⊥AB;HN⊥AC$
$⇒\widehat{HMA}=\widehat{HNA}=90^o$
$⇒\widehat{HMA}+\widehat{HNA}=180^o$
$⇒$ Tứ giác $AMHN$ nội tiếp (Tổng 2 góc đối $=180^o$)
b, Xét tam giác $AHB$ vuông tại $H$
Đường cao $HM$ (do $HM⊥AB$)
Nên $AH^2=AM.AB(1)$
Xét tam giác $AHC$ vuông tại $H$
Đường cao $HN$ (do $HN⊥AB$)
Nên $AH^2=AN.AC(2)$
Từ $(1)(2)⇒AM.AB=AN.AC$
$⇒\dfrac{AM}{AC}=\dfrac{AN}{AB}$
Xét tam giác $AMN$ và tam giác $ACB$ có:
$\dfrac{AM}{AC}=\dfrac{AN}{AB}$
$\widehat{A}$ chung
$⇒$ tam giác $AMN$ $\backsim$ tam giác $ACB(c.g.c)$
(đpcm)
c, tam giác $AMN$ $\backsim$ tam giác $ACB$
$⇒\widehat{ANM}=\widehat{ABC}$
Xét $(O)$ có: $\widehat{ABC}=\widehat{AEC}$ (các góc nội tiếp cùng chắn cung $AC$)
Nên $\widehat{ANM}=\widehat{AEC}$
Hay $\widehat{ANI}=\widehat{IEC}$
$⇒$ Tứ giác $CEIN$ nội tiếp (góc ngoài tại 1 đỉnh = góc trong đỉnh đối diện)
c, Ta có: $\widehat{ANM}=\widehat{ABC}$
Mà $\widehat{ABC}+\widehat{AKC}=180^o$
do tứ giác $ABCK$ nội tiếp $(O)$
Nên $\widehat{ANM}+\widehat{AKC}=180^o$
Mà $\widehat{ANM}+\widehat{ANK}=180^o$
Nên $\widehat{AKC}=\widehat{ANK}$
Xét tam giác $AKC$ và tam giác $ANK$ có:
$\widehat{AKC}=\widehat{ANK}$
$\widehat{A}$ chung
nên tam giác $AKC$ $\backsim$ tam giác $ANK(g.g)$
$⇒\dfrac{AK}{AN}=\dfrac{AC}{AK}$
$⇒AK^2=AN.AC$
mà $AH^2=AN.AC(cmt)$
$⇒AK^2=AH^2$
hay $AK=AH$
suy ra tam giác $AHK$ cân tại $A$
Đúng 3
Bình luận (1)
Nguyễn Lê Phước Thịnh
Akai Haruma Trần Đức Mạnh Nguyễn Việt Lâm
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. Từ điểm M trên tiếp tuyến Ax của nửa đường tròn vẽ tiếp tuyến thứ hai MC với nửa đường tròn. Kẻ CH vuông góc với AB, MB cắt nửa đường tròn (O) tại Q và cắt CH tại N. Chứng minh: a) MO vuông góc AC. b) \(MA^2\)=MQ.MB c) MO cắt AC tại I. Chứng minh: A, I, Q, M cùng thuộc một đường tròn. d) NC = NH.
Cho nửa đường tròn tâm O đường kính AB. Từ điểm M trên tiếp tuyến Ax của nửa đường tròn vẽ tiếp tuyến thứ hai MC với nửa đường tròn. Kẻ CH vuông góc với AB, MB cắt nửa đường tròn (O) tại Q và cắt CH tại N. Chứng minh: a) MO vuông góc AC. b) MA^2MQ.MB c) MO cắt AC tại I. Chứng minh: A, I, Q, M cùng thuộc một đường tròn. d) NC NH.
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Từ điểm M trên tiếp tuyến Ax của nửa đường tròn vẽ tiếp tuyến thứ hai MC với nửa đường tròn. Kẻ CH vuông góc với AB, MB cắt nửa đường tròn (O) tại Q và cắt CH tại N. Chứng minh: a) MO vuông góc AC. b) MA\(^2\)=MQ.MB c) MO cắt AC tại I. Chứng minh: A, I, Q, M cùng thuộc một đường tròn. d) NC = NH.
Cho tam giác ABC nhọn nội tiếp đường tròn (O) (AB<AC). Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn, AD cắt BC tại E. Gọi K là chân đường vuông góc kẻ từ C đến ADa) C/m 4 điểm A, H, K, C cùng thuộc một đường tròn
Xem chi tiết
a: Xét tứ giác AHKC có \(\widehat{AHC}=\widehat{AKC}=90^0\)
nên AHKC là tứ giác nội tiếp
=>A,H,K,C cùng thuộc một đường tròn
Đúng 0
Bình luận (0)