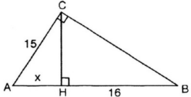
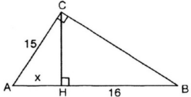
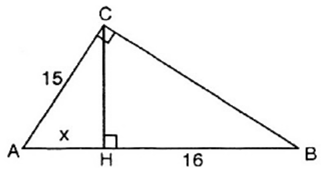
cho tam giác ABC vuông tại C.kẻ đường cao CH chia đoạn AB thành 2 đoạn thẳng AH và HB.biết AC=15cm,HB=16cm.Tính diện tích tam giác ABC

Những câu hỏi liên quan
Tam giác ABC vuông tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC.
Tam giác ABC vuông tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC.
Tam giác ABC vuông góc tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC ?
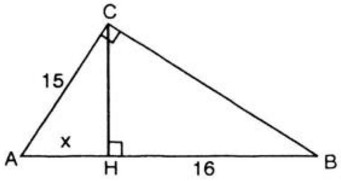
Đặt AH = x (x > 0)
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có: AC2 = AB.AH
hay 152 = (x + 16)x ⇔ x2 + 16x -225 = 0
Giải phương trình, ta được x1 = 9 (thỏa mãn); x2 = -25 (loại)
Vậy AH = 9 (cm)
Ta có: HC2 = AH. HB = 9. 16 = 144
⇒ HC = 12 (cm)
Vậy diện tích tam gaics ABC là:
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C, Ac=15. Đường cao AH chia AB thành 2 đoạn thẳng AH và HB với HB=16. Tính diện tích ABC
Đặt AH = x ( x > 0 ) , ta có :
\(AC^2=AH.AB\)
\(\Leftrightarrow15^2=x\left(x+16\right)\)
\(\Leftrightarrow x^2+16x-225=0\)
Giải phương trình , ta được : \(x_1=9\)
\(x_2=-25\)( loại )
Vậy AH = 9 , suy ra :
\(CH=\sqrt{AC^2-AH^2}=\sqrt{15^2-9^2}=12\)
=> Diện tích tam giác ABC là :
\(S_{ABC}=\frac{1}{2}AB.CH=\frac{1}{2}\left(9+16\right).12=150\left(cm^{^2}\right)\)
Tam giác ABC vuông tại C có AC = 15 cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16 cm. Tính diện tích tam giác ABC.
Cho tam giác ABC vuông tại A có đường cao AH.Biết AC=15cm; HB=16cm.Tính BC;AB;AH;CH
Ta có: \(AC^2=CH\cdot BC\)
\(\Leftrightarrow CH^2+16HC-225=0\)
\(\Leftrightarrow CH^2+25HC-9HC-225=0\)
\(\Leftrightarrow CH=9\left(cm\right)\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=15^2-9^2=144\)
hay AH=12cm
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20cm
Ta có: BC=BH+HC
nên BC=9+16=25cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH. Biết AB=15cm;HC=16cm.Tính HB,BC,AH,AC.
theo hệ thức lượng tam giác vuông
AC^2 = HC*BC = 16*BC (1)
AH^2 = HC*BH = 16*BH (2)
1/AH^2 = 1/AC^2 + 1/AB^2 (3)
thay 1,2 vào 3:
1/16*BH = 1/16*BC + 1/15^2 (4)
mặt khác:
BH = BC - HC = BC -16
thay vào 4:
1/16*(BC -16) = 1/16*BC + 1/225
<=> 1/(BC - 16) - 1/BC = 16/225
<=> (BC -BC +16)/((BC - 16)*BC) =16/225
<=> BC^2 - 16*BC - 225 = 0
=> BC = 25 (thỏa mãn) BC = -9 (loại)
thay vào 1 ta có AC = 20 cm
2 ta có AH = 12 cm
Cố lên bạn nha!
Đúng 1
Bình luận (1)
Đặt HB=x(cm,x>0) => BC=HB+HC=x+16
Ta có: Tam giác ABC vuông tại A có AH là đường cao
=>AB2=HB.BC
=>152=x.(x+16)
=>225=x2+16x
=>x2+16x-225=0
=>x2+25x-9x-225=0
=>x.(x+25)-9.(x+25)=0
=>(x+25).(x-9)=0
=>x=-25(loại) hay x=9(nhận)
Vậy HB=9(cm)
Ta có: AH2=HB.HC(hệ thức lượng)
=>AH2=9.16=144
=AH=12(cm)
Ta có: AC2=HC.BC(hệ thức lượng)
=>AC2=16.25=400
=>AC=20(cm)
Ta có: BC=HB+HC=9+16=25(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.
A. 15cm
B. 12cm
C. 10cm
D. 8cm
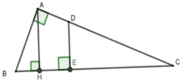
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.
Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)
Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = 18 25 (2).
Từ (1) và (2) suy ra
S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 3
Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên
S D E C : S A H C = ( E C H C ) 2 (4)
Từ (3) và (4) suy ra E C H C = 5 6 tức là E C 18 = 5 6 => EC = 15cm.
Đáp án: A
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH = 5cm. Biết CH = 6cm. tính:
a) AB, AC,BC và BH?
b) Diện tích tam giác ABC
Bài2: Cho tam giác ABC vuông tại A, đường cao AH; AB = 15cm; BC = 25cm. BTính:
a) AC,AH, HC và BH?
b) Diện tích tam giác ABC
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
Đúng 3
Bình luận (0)