Lời giải:
$(y+2)(x^2+1)=2x^3+3x+1$

$\Leftrightarrow y+2=\frac{2x^3+3x+1}{x^2+1}$
\(=\frac{2x(x^2+1)+(x+1)}{x^2+1}=2x+\frac{x+1}{x^2+1}\)

$\Leftrightarrow y+2-2x=\frac{x+1}{x^2+1}$

 $x,y$ nguyên nên $y+2-2x$ nguyên $\Leftrightarrow \frac{x+1}{x^2+1}$ nguyên 

$\Leftrightarrow x+1\vdots x^2+1$

Khi đó có 2 TH xảy ra: 

TH1: $x+1=0$

$\Leftrightarrow x=-1$

Thay vô pt ban đầu suy ra $y=-4$ (tm) 

TH2: $x+1\neq 0$. Khi đó $x+1\vdots x^2+1$
$\Rightarrow x+1\geq x^2+1$
$\Leftrightarrow x^2-x\leq 0\Leftrightarrow x(x-1)\leq 0$

$\Leftrightarrow 0\leq x\leq 1$

Vì $x$ nguyên nên $x=0$ hoặc $x=1$. Thử vào pt ban đầu suy ra $(x,y)=(0,1), (1,3)$

Vậy.........

Ctrl F5

vào trang cá nhân bấm phím ctrl+ F5

lâu lâu nó bị lỗi xíu á, đợi một chút là nó cập nhật thôi

\(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|4\overrightarrow{MB}-\overrightarrow{MC}\right|\)

⇔ \(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|3\overrightarrow{MB}+\overrightarrow{CB}\right|\) (1)

Trên cạnh AB lấy O sao cho \(\dfrac{OA}{OB}=\dfrac{1}{2}\)

⇒ \(2\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}\)

Trên cạnh tia đối của tia BC lấy E sao cho \(\dfrac{EB}{BC}=\dfrac{1}{3}\)

⇒ \(3\overrightarrow{EB}+\overrightarrow{CB}=\overrightarrow{0}\)

Vậy (1) ⇒ \(\left|3\overrightarrow{MO}+2\overrightarrow{OA}+\overrightarrow{OB}\right|=\left|3\overrightarrow{ME}+3\overrightarrow{EB}+\overrightarrow{CB}\right|\)

⇒ 3MO = 3ME

⇒ MO = ME

⇒ M nằm trên đường trung trực của OE 

d. G thuộc Ox nên \(G\left(2;0\right)\)

d qua G nên:

\(2\left(m^2-3m\right)+2m-5=0\)

\(\Leftrightarrow2m^2-4m-5=0\Rightarrow m=\dfrac{2\pm\sqrt{14}}{2}\)

b.

H thuộc Oy nên: \(H\left(0;3\right)\)

d qua H nên:

\(0\left(m^2-3m\right)+2m-5=3\)

\(\Rightarrow2m=8\Rightarrow m=4\)

ta co 2x<=x^2+1 cosi

\(\sqrt{2x-1}\le\sqrt{x^2+1-1}=\sqrt{x^2}\)=|x|

..............................

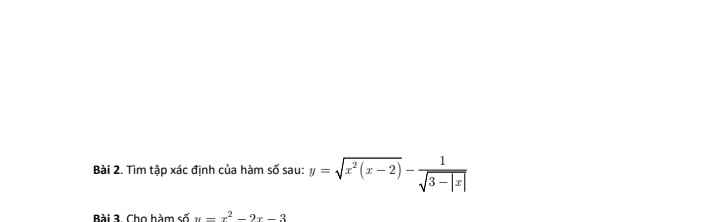
Bài 2: 

ĐKXĐ: \(\left\{{}\begin{matrix}-3< x< 3\\x\ge2\end{matrix}\right.\Leftrightarrow2\le x< 3\)