Cho \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\). CMR : \(\dfrac{a.c}{b.d}\)=\(\dfrac{a^2+c^2}{b^2+d^2}\)

Những câu hỏi liên quan
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\)
CMR: \(\dfrac{a.c}{b.d}\) = \(\dfrac{a^2+c^2}{b^2+d^2}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\\ \dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\\ \Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{ac}{bd}\)
Đúng 0
Bình luận (0)
cho \(b^2\)=a.c; \(c^2\)= b.d. CMR: \(\left(\dfrac{a.b.c}{b.c.d}\right)\)^2=\(\dfrac{a}{d}\)
Đề sai rồi bạn. Phải thay "^2" bằng "^3" mới đúng.
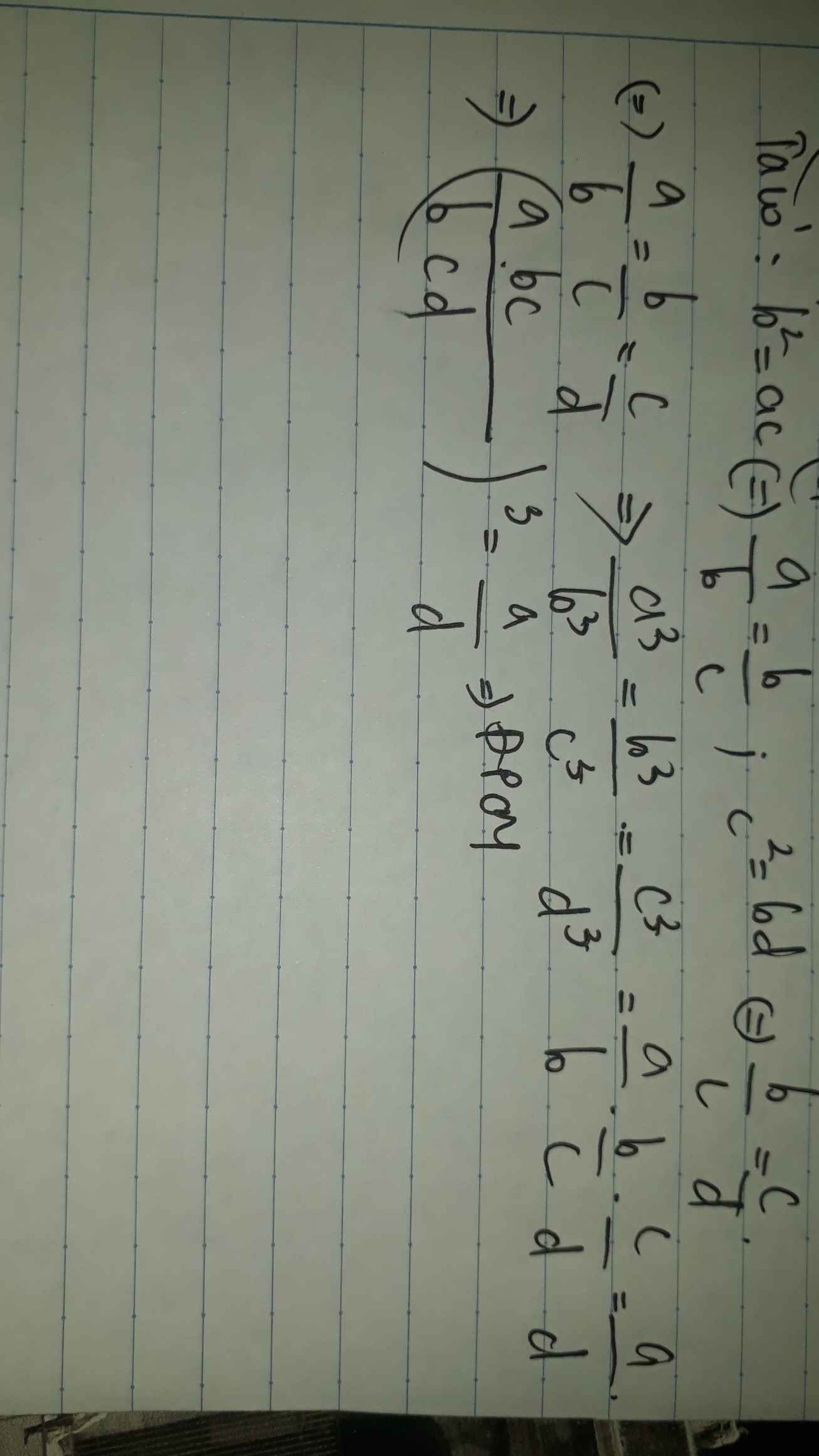
Đúng 2
Bình luận (1)
cho \(\dfrac{a}{b}=\dfrac{c}{d}\)(b,d≠0) chứng tỏ rằng \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{a.c}{b.d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a^2}{b^2}=\dfrac{c^2}{d^2}=\dfrac{a^2+c^2}{b^2+d^2}\) (1)
Lại có vì : \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a^2}{b^2}=\dfrac{ac}{bd}\) (2)
Từ (1) và (2) => ĐPCM
Đúng 0
Bình luận (0)
cho dfrac{a}{b} dfrac{c}{d} cm rằng a) dfrac{a}{a-b} dfrac{c}{c-d} b)dfrac{a}{b} dfrac{a+c}{b+d} c) dfrac{a}{3a+d} dfrac{c}{3c+d} d)dfrac{a.c}{b.d} dfrac{a^2+c^2}{b^2+c^2} e)dfrac{a.b}{c.d} dfrac{a^2-b^2}{c^2-d^2} f)dfrac{a.b}{c.d} dfrac{left(a-bright)^2}{left(c-dright)^2} mn giúp mk vs ạ! thanks
Đọc tiếp
cho \(\dfrac{a}{b}\) =\(\dfrac{c}{d}\) cm rằng
a) \(\dfrac{a}{a-b}\) =\(\dfrac{c}{c-d}\) b)\(\dfrac{a}{b}\) =\(\dfrac{a+c}{b+d}\) c) \(\dfrac{a}{3a+d}\) =\(\dfrac{c}{3c+d}\) d)\(\dfrac{a.c}{b.d}\) =\(\dfrac{a^2+c^2}{b^2+c^2}\) e)\(\dfrac{a.b}{c.d}\) =\(\dfrac{a^2-b^2}{c^2-d^2}\) f)\(\dfrac{a.b}{c.d}\) =\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
mn giúp mk vs ạ! thanks
a) Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Leftrightarrow\dfrac{b}{a}-1=\dfrac{d}{c}-1\)
\(\Leftrightarrow\dfrac{b-a}{a}=\dfrac{d-c}{c}\)
\(\Leftrightarrow\dfrac{a-b}{a}=\dfrac{c-d}{c}\)
\(\Leftrightarrow\dfrac{a}{a-b}=\dfrac{c}{c-d}\)(đpcm)
Đúng 2
Bình luận (0)
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\),Chứng minh \(\dfrac{a^2}{b^2}=\dfrac{a.c}{b.d}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=bk\),\(c=dk\)
\(\dfrac{a^2}{b^2}=\dfrac{bk^2}{b^2}=k^2\left(1\right)\)
\(\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=k^2\left(2\right)\)
Từ (1) và (2)=>\(\dfrac{a^2}{b^2}=\dfrac{ac}{bd}\)(đpcm)
Đúng 0
Bình luận (0)
Đặt \(\dfrac{a}{b}=k;\dfrac{c}{d}=k\)
\(\Rightarrow a=kb;c=kd\)
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{bk^2}{b^2}=k^2\)
\(\Rightarrow\dfrac{ac}{bd}=\dfrac{bkdk}{bd}=k^2\)
Từ các chứng minh trên cho ta thấy
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{a.c}{b.d}\)
Đúng 0
Bình luận (0)
Đặt:
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) \(\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{bk^2}{b^2}=k^2\)
\(\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=\dfrac{k^2bd}{bd}=k^2\)
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{ac}{bd}\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
Cho \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh :
a) \(\dfrac{a.c}{b.d}=\dfrac{a^2-c^2}{b^2-d^2}\)
b) \(\dfrac{a^2}{b^2}=\dfrac{3a^2-2ac}{3b^2-2bd}\)
Ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}=\dfrac{3a}{3b}=\dfrac{2c}{2d}=\dfrac{3a-2c}{3b-2d}\)
a/ \(\dfrac{a.c}{b.d}=\dfrac{\left(a+c\right).\left(a-c\right)}{\left(b+d\right).\left(b-d\right)}=\dfrac{a^2-c^2}{b^2-d^2}\)
b/ \(\dfrac{a^2}{b^2}=\dfrac{a}{b}.\dfrac{3a-2c}{3b-2d}=\dfrac{3a^2-2ac}{3b^2-2bd}\)
Đúng 0
Bình luận (0)
Cho các số a,b,c,d ≠ 0 và \(b^2=a.c\) ; \(c^2=b.d\) ; \(b^3+c^3+d^3\ne0\). C/m rằng :\(\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}=\dfrac{a}{d}\)
\(\left.\begin{matrix} b^2=ac\Rightarrow \dfrac{a}{b}=\dfrac{b}{c} \\c^2=bd \Rightarrow \dfrac{b}{c}=\dfrac{c}{d}\end{matrix}\right\}\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\\ \Rightarrow\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}\)
Áp dụng t/c của DTSBN , ta có :
\(\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}\\ \Rightarrow\dfrac{a^3}{b^3}=\dfrac{a^3+b^3+c^3}{d^3+c^3+d^3}\left(1\right)\)
Có `a^3/b^3=a/b*a/b*a/b=a/b*b/c*c/d=a/d` ( do `a/b=b/c=c/d` )`(2)
Từ `(1);(2)=>` \(\dfrac{a}{d}=\dfrac{a^3+b^3+c^3}{b^3+c^3+d^3}\)
Đúng 2
Bình luận (0)
cho \(b^2=a.c-a^2=b.d\)
c/m:\(\dfrac{a^3+b^3-c^3}{b^3+c^2-d^3}=\left(\dfrac{a+b-c}{b+c-d}\right)^2\)
\(b^2=a.c\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}\left(1\right)\)
\(c^2=b.d\)
\(\Rightarrow\dfrac{b}{c}=\dfrac{c}{d}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{a+b-c}{b+c-d}\)
\(\Rightarrow\left(\dfrac{a}{b}\right)^3=\left(\dfrac{b}{c}\right)^3=\left(\dfrac{c}{d}\right)^3=\left(\dfrac{a+b-c}{b+c-d}\right)^3\)
\(=\dfrac{a^3}{b^3}=\dfrac{b^3}{c^3}=\dfrac{c^3}{d^3}=\left(\dfrac{a+b-c}{b+c-d}\right)^3=\dfrac{a^3+b^3-c^3}{b^3+c^3-d^3}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Bài 1:Tìm 3 số a,b,c biết
dfrac{3a-2b}{5}dfrac{2c-5a}{3}dfrac{5b-3c}{2} và a+b+c -50
Bài 2: Chứng minh rằng:Nếu các số a,b,c,d thỏa mãn:
[ab(ab-2cd)+c2.d2].[ab(ab-2)+2(ab+1)] 0
Thì a,b,c,d lập thành một tỉ lệ thức
Bài 3:Cho b2 a.c; c2b.d (c,b,dne0 và b+cne0 ; b3+d3ne d^3 )
CMR dfrac{a^3+b^3-c^3}{b^3+c^3-d^3}left(dfrac{a+b-c}{b+c-d}right)^3
Bài 4: Cho b2 a.c (a,cne0 )
CMR dfrac{a}{c}left(dfrac{2016a-2017b}{2016b-2017c}right)^2
Đọc tiếp
Bài 1:Tìm 3 số a,b,c biết
\(\dfrac{3a-2b}{5}=\dfrac{2c-5a}{3}=\dfrac{5b-3c}{2}\) và a+b+c= -50
Bài 2: Chứng minh rằng:Nếu các số a,b,c,d thỏa mãn:
[ab(ab-2cd)+c2.d2].[ab(ab-2)+2(ab+1)] =0
Thì a,b,c,d lập thành một tỉ lệ thức
Bài 3:Cho b2= a.c; c2=b.d (c,b,d\(\ne0\) và b+c\(\ne0\) ; b3+d3\(\ne d^3\) )
CMR \(\dfrac{a^3+b^3-c^3}{b^3+c^3-d^3}=\left(\dfrac{a+b-c}{b+c-d}\right)^3\)
Bài 4: Cho b2 = a.c (a,c\(\ne0\) )
CMR \(\dfrac{a}{c}=\left(\dfrac{2016a-2017b}{2016b-2017c}\right)^2\)


























