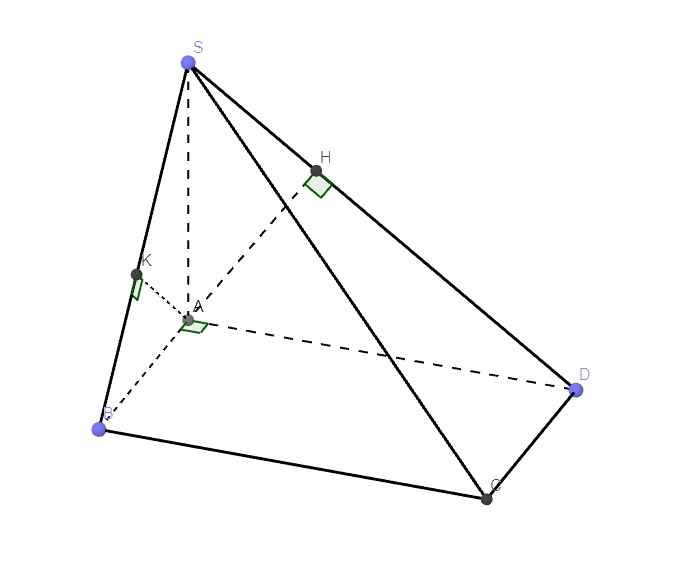
cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB=a, SA vuông góc với đáy =a.. tính ((SAD);(SBC))

Những câu hỏi liên quan
Cho hình chóp SABCD có đáy hình chữ nhật AB=a, BC=2a, SA vuông góc với ABCD, SA= acăn5. Tính khoảng cách từ C đến mp SAD.
Theo đề có:
\(\left\{{}\begin{matrix}CD\perp AD\\CD\perp SA\end{matrix}\right.\)
=> \(CD\perp\left(SAD\right)\)
<=> \(d\left(C,\left(SAD\right)\right)=CD=a\)
`HaNa♬`
Đúng 1
Bình luận (0)
MỌI NGƯỜI GIÚP MÌNH VỚI MÌNH CẢM ƠN NHIỀU
Bài 5. Cho hình chóp SABCD có đáy ABCD là hình chữ nhật; mặt phẳng (SAB) và (SAD)cùng vuông góc với đáy. Biết AB=a;AD=2a a. Cmr SA (ABCD): b. Biết góc giữa SD với mặt phẳng (ABCD) bằng 60° .Tính SA theo a c.Tính khoảng cách từ điểm A đến mặt phẳng (SCD) d. Gọi I là trung điểm AD, Tính khoảng cách từ điểm I đến mặt phẳng (SBC).
Mọi người giúp m vs ạ
Bài 5. Cho hình chóp SABCD có đáy ABCD là hình chữ nhật; mặt phẳng (SAB) và (SAD)cùng vuông góc với đáy. Biết AB=a;AD=2a
a. Cmr SA (ABCD)
b. Biết góc giữa SD với mặt phẳng (ABCD) bằng 60° .Tính SA theo a
c.Tính khoảng cách từ điểm A đến mặt phẳng (SCD)
d. Gọi I là trung điểm AD, Tính khoảng cách từ điểm I đến mặt phẳng (SBC).
a. Do \(\left\{{}\begin{matrix}SA=\left(SAB\right)\cap\left(SAD\right)\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
b.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD) \(\Rightarrow\widehat{SDA}=60^0\)
\(tan\widehat{SDA}=\dfrac{SA}{AD}\Rightarrow SA=AD.tan\widehat{SDA}=2a\sqrt{3}\)
c.
Từ A kẻ \(AH\perp SD\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SCD\right)\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(AH=AD.sin\widehat{SDA}=2a.sin60^0=a\sqrt{3}\)
d.
Ta có: \(AI||BC\Rightarrow d\left(I;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)\)
Trong tam giác vuông SAB, kẻ \(AK\perp SB\)
Tương tự câu c, dễ dàng chứng minh \(AK\perp\left(SBC\right)\Rightarrow AK=d\left(A;\left(SBC\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{AK^2}=\dfrac{1}{AB^2}+\dfrac{1}{SA^2}=\dfrac{13}{12a^2}\Rightarrow AK=\dfrac{2a\sqrt{39}}{13}\)
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật SA vuông góc với ABCD. AE và AF là đường cao của tam giác SAB và SAD, SC vuông góc với?
Bạn coi lại đề, sao lại có 2 cái AF là đường cao của 2 tam giác khác nhau thế kia?
Đúng 2
Bình luận (0)
Chóp SABCD , ABCD là hình chữ nhật tâm O SA=5a ; AB=2a ; AD=a căn 3 ; SA vuông góc với đáy a) Cm BC vuông góc (SAB) ; CD vuông góc (SAD ) ; (SCD) vuông góc (SAD) b) Tính góc (SC:SAD) ; (SC:SAD) ; (SC:ABCD) c) Tính khoảng cách từ A đến (SBC) và d(A,(SCD)) d)Tính góc giữa 2 mp (SBD) và (ABCD) ; (SCD) và (ABCD)
a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ
Đúng 1
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, ABa. Cạnh bên SA vuông góc với đáy và SAa. Góc giữa đường thẳng SB và CD là: A.
90
o
B.
60
o
C.
30
o
D.
45
o
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, AB=a. Cạnh bên SA vuông góc với đáy và SA=a. Góc giữa đường thẳng SB và CD là:
A. 90 o
B. 60 o
C. 30 o
D. 45 o
Chọn D.
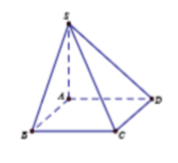
Ta có AB//CD
⇒ S B ; C D ^ = S B ; A B ^ = S B A ^ = 45 o d o ∆ S B A c â n
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với (ABCD) và SA = 2a. 1. Chứng minh (SCD) vuông góc với (SAD) 2. Tính d(A, (SCD))
1: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SCD) vuông góc (SAD)
Đúng 1
Bình luận (0)
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Bạn chỉ nên đăng 1 bài 1 lần thôi, tránh làm loãng box toán!
Đúng 1
Bình luận (0)
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Lời giải:
Vì $SA\perp (ABCD)$ nên
$60^0= \angle (SC, (ABCD))=\angle (SC, AC)=\widehat{SCA}$
Ta có:
$AC=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
$\frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{15}a$
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}$
$=\frac{1}{3}.\sqrt{15}a.a.2a=\frac{2\sqrt{15}}{3}a^3$
Đúng 2
Bình luận (0)
Cho hình chóp SABCD đáy ABCD là hình chữ nhật tâm I ,AB =a, BC=a căn 3 .Tam giác SIA cân tại S . (SAD) vuông góc với đáy .góc giữa SD và (ABCD) = 60* .Tính thể tích khối chóp SABCI?