Mọi người giúp m vs ạ
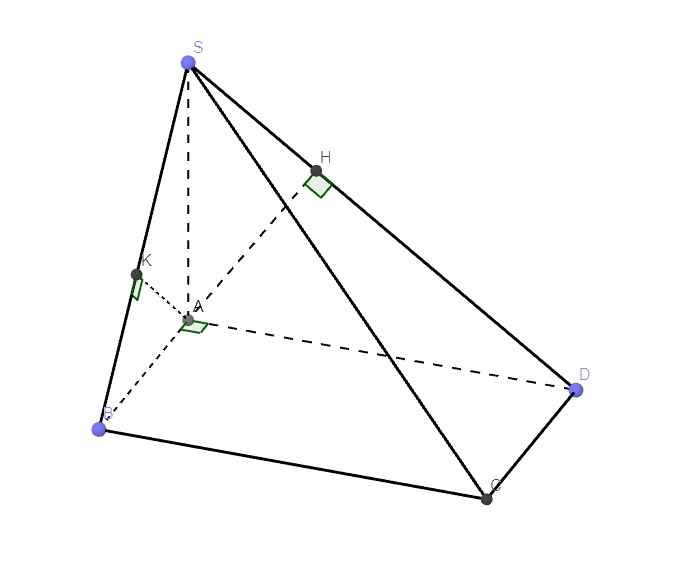
Bài 5. Cho hình chóp SABCD có đáy ABCD là hình chữ nhật; mặt phẳng (SAB) và (SAD)cùng vuông góc với đáy. Biết AB=a;AD=2a
a. Cmr SA (ABCD)
b. Biết góc giữa SD với mặt phẳng (ABCD) bằng 60° .Tính SA theo a
c.Tính khoảng cách từ điểm A đến mặt phẳng (SCD)
d. Gọi I là trung điểm AD, Tính khoảng cách từ điểm I đến mặt phẳng (SBC).
a. Do \(\left\{{}\begin{matrix}SA=\left(SAB\right)\cap\left(SAD\right)\\\left(SAB\right)\perp\left(ABCD\right)\\\left(SAD\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
b.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu vuông góc của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD) \(\Rightarrow\widehat{SDA}=60^0\)
\(tan\widehat{SDA}=\dfrac{SA}{AD}\Rightarrow SA=AD.tan\widehat{SDA}=2a\sqrt{3}\)
c.
Từ A kẻ \(AH\perp SD\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SCD\right)\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(AH=AD.sin\widehat{SDA}=2a.sin60^0=a\sqrt{3}\)
d.
Ta có: \(AI||BC\Rightarrow d\left(I;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)\)
Trong tam giác vuông SAB, kẻ \(AK\perp SB\)
Tương tự câu c, dễ dàng chứng minh \(AK\perp\left(SBC\right)\Rightarrow AK=d\left(A;\left(SBC\right)\right)\)
Hệ thức lượng:
\(\dfrac{1}{AK^2}=\dfrac{1}{AB^2}+\dfrac{1}{SA^2}=\dfrac{13}{12a^2}\Rightarrow AK=\dfrac{2a\sqrt{39}}{13}\)